[Image1]
Introduction
Hey it's a me again @drifter1!
Today we continue with my mathematics series about Signals and Systems to talk about the Properties of the Z Transform.
So, without further ado, let's dive straight into it!
Z Transform Recap
The Z Transform is a generalization of the Discrete-Time Fourier Transform. Basically, the complex exponentials that are used as building blocks for signals are replaced by more general exponentials with complex base. This allows the Z Transform to converge for signals/sequences that normally don't converge using the Fourier Transform, and can be thought of as some kind of exponential weighting.


The Fourier and Z Transform are related in the following manner:

Z Transform Properties
Similar to all other Transforms that have been covered throughout this series, the Z Transform also satisfies many properties. These properties are basically the same as the Discrete-Time Fourier Transform (or even the Laplace Transform), but have a few differences in the math. Of course, similar to the Laplace Transform, all these properties also affect the ROC, and so the complete definition of the outcome, algebraic equation and ROC, will be the main topic of this article.
Linearity
Consider the following two Z Transforms of Discrete-Time signals:

The linear combination of those signals leads to the following Z Transform:

So, the ROC of the result is equal to the intersection of the two individual ROCs. Let's note that the ROC might also additional regions, and so this ROC is basically the least for which the Z Transform converges. More specifically, if the linear combination leads to additional zeros or poles, these will of course have to be included in the ROC.
Time-Shifting
Let's now consider the following Z Transform:
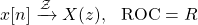
The time-shifted (sample-shifted) signal x[n - n0] has the following Z Transform:
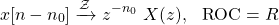
The ROC is basically the same as the original signal, but additional regions might be included at z = 0 or infinity. This depends on how the scaling by z -n0 affects the pole-zero pattern.
Time-Scaling
In Discrete-Time, because samples are only taken at integer indexes, time-scaling leads to the introduction of zeros between the samples. As such, scaling by 1 / k introduces k - 1 zeros between the individual samples of the original signal. Mathematically:

Now for the Z Transform. The algebraic expression and ROC are:
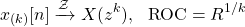
So, if z is a point in the original ROC then z 1 / k is a part of the resulting ROC. The same is also true for poles and zeros. As such, if z = a is a pole (zero) then z = a 1 / k will also be a pole (zero) in the resulting pole-zero pattern.
Time-Reversal
Reversing a signal in time, also leads to an interesting result. The Z Transform of the signal x[-n], is as follows:
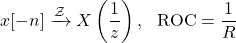
So, if z0 is a part of the original ROC, then 1 / z0 will be part of the resulting ROC.
z-Domain Scaling
The equivalent of frequency shifting in the case of the Z Transform is known as z-Domain Scaling. Of course frequency scaling in the Time-Domain leads to scaling in the z-Domain.
So, Multiplying a given signal x[n] by z0n yields the following result:

So, if the original ROC contained z, then the resulting ROC will contain |z0| z. The same also applies for the poles and zeros.
A special case is z0 = e jω0, which leads to a rotation of the ROC by an angle of ω0. In other words, the pole-zero pattern is rotated by an angle of ω0. Mathematically:

And if we get even more generic with a z0 = r0 e jω0, then in addition to being rotated by ω0, the poles and zeros are also scaled in value by r0.
Conjugation
The Z Transform also satisfies conjugation. As such, the Z Transform of the conjugate x*[n] is:

If the signal x[n] is real, then its possible to conclude that:

Which means that if the original ROC has a pole (or zero) at z = z0, then there will also be a pole (or zero) at the conjugate point z = z0*.
Convolution
Next up is convolution, which is a very useful property. This property allows us to turn the complicated convolution sum into a simple multiplication in the z-Domain.
Mathematically, the Z Transform of the convolution of two signals is as follows:

So, the ROC is equal to the intersection of the two individual ROCs, with the possibility of including additional poles-zeros depending on the result of the multiplication.
Differentation in the z-Domain
Differentation in the z-Domain is another quite useful property, which is basically the multiply-by-n property.
Algebraically, the resulting Z Transform is:
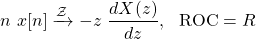
which is a direct consequences of differentiating both sides of the z Transform equation.
Initial and Final Value Theorems
The Z Transform also satisfies similar initial and final value theorems to the Laplace Transform.
The initial value theorem states that for any causal signal x[n]:

As such, this theorem is useful for finding the initial value of a signal without taking the inverse Z Transform.
Whilst, the final value theorem states that for any causal signal x[n]:

Similarly, this theorem is useful for finding the final value of a signal withotu taking the inverse Z Transform.
RESOURCES:
References
Images
Mathematical equations used in this article were made using quicklatex.
Block diagrams and other visualizations were made using draw.io and GeoGebra
Previous articles of the series
Basics
- Introduction → Signals, Systems
- Signal Basics → Signal Categorization, Basic Signal Types
- Signal Operations with Examples → Amplitude and Time Operations, Examples
- System Classification with Examples → System Classifications and Properties, Examples
- Sinusoidal and Complex Exponential Signals → Sinusoidal and Exponential Signals in Continuous and Discrete Time
LTI Systems and Convolution
- LTI System Response and Convolution → Linear System Interconnection (Cascade, Parallel, Feedback), Delayed Impulses, Convolution Sum and Integral
- LTI Convolution Properties → Commutative, Associative and Distributive Properties of LTI Convolution
- System Representation in Discrete-Time using Difference Equations → Linear Constant-Coefficient Difference Equations, Block Diagram Representation (Direct Form I and II)
- System Representation in Continuous-Time using Differential Equations → Linear Constant-Coefficient Differential Equations, Block Diagram Representation (Direct Form I and II)
- Exercises on LTI System Properties → Superposition, Impulse Response and System Classification Examples
- Exercise on Convolution → Discrete-Time Convolution Example with the help of visualizations
- Exercises on System Representation using Difference Equations → Simple Block Diagram to LCCDE Example, Direct Form I, II and LCCDE Example
- Exercises on System Representation using Differential Equations → Equation to Block Diagram Example, Direct Form I to Equation Example
Fourier Series and Transform
- Continuous-Time Periodic Signals & Fourier Series → Input Decomposition, Fourier Series, Analysis and Synthesis
- Continuous-Time Aperiodic Signals & Fourier Transform → Aperiodic Signals, Envelope Representation, Fourier and Inverse Fourier Transforms, Fourier Transform for Periodic Signals
- Continuous-Time Fourier Transform Properties → Linearity, Time-Shifting (Translation), Conjugate Symmetry, Time and Frequency Scaling, Duality, Differentiation and Integration, Parseval's Relation, Convolution and Multiplication Properties
- Discrete-Time Fourier Series & Transform → Getting into Discrete-Time, Fourier Series and Transform, Synthesis and Analysis Equations
- Discrete-Time Fourier Transform Properties → Differences with Continuous-Time, Periodicity, Linearity, Time and Frequency Shifting, Conjugate Summetry, Differencing and Accumulation, Time Reversal and Expansion, Differentation in Frequency, Convolution and Multiplication, Dualities
- Exercises on Continuous-Time Fourier Series → Fourier Series Coefficients Calculation from Signal Equation, Signal Graph
- Exercises on Continuous-Time Fourier Transform → Fourier Transform from Signal Graph and Equation, Output of LTI System
- Exercises on Discrete-Time Fourier Series and Transform → Fourier Series Coefficient, Fourier Transform Calculation and LTI System Output
Filtering, Sampling, Modulation, Interpolation
- Filtering → Convolution Property, Ideal Filters, Series R-C Circuit and Moving Average Filter Approximations
- Continuous-Time Modulation → Getting into Modulation, AM and FM, Demodulation
- Discrete-Time Modulation → Applications, Carriers, Modulation/Demodulation, Time-Division Multiplexing
- Sampling → Sampling Theorem, Sampling, Reconstruction and Aliasing
- Interpolation → Reconstruction Procedure, Interpolation (Band-limited, Zero-order hold, First-order hold)
- Processing Continuous-Time Signals as Discrete-Time Signals → C/D and D/C Conversion, Discrete-Time Processing
- Discrete-Time Sampling → Discrete-Time (or Frequency Domain) Sampling, Downsampling / Decimation, Upsampling
- Exercises on Filtering → Filter Properties, Type and Output
- Exercises on Modulation → CT and DT Modulation Examples
- Exercises on Sampling and Interpolation → Graphical/Visual Sampling and Interpolation Examples
Laplace and Z Transforms
- Laplace Transform → Laplace Transform, Region of Convergence (ROC)
- Laplace Transform Properties → Linearity, Time- and Frequency-Shifting, Time-Scaling, Complex Conjugation, Multiplication and Convolution, Differentation in Time- and Frequency-Domain, Integration in Time-Domain, Initial and Final Value Theorems
- LTI System Analysis using Laplace Transform → System Properties (Causality, Stability) and ROC, LCCDE Representation and Laplace Transform, First-Order and Second-Order System Analysis
- Exercises on the Laplace Transform → Laplace Transform and ROC Examples, LTI System Analysis Example
- Z Transform → Z Transform, Region of Convergence (ROC), Inverse Z Transform
Final words | Next up
And this is actually it for today's post!
Next time we will get into how the Z Transform is useful in LTI System Analysis...
See Ya!

Keep on drifting!
