In this video I look further into the Tengri 137 cryptic series of alien math puzzles, and this time revisit the calculation of the Tengri “Name” that covered in Part 7. In a bizarre twist, the popular YouTuber Defango did a hit-piece on me claiming that I was “cheating” by using online “tools” and “calculators”, particularly the #AMAZING Wolfram Alpha calculator…. This is particularly strange because it was only after Part 7 in which I was accused of “cheating”, even AFTER Tengri already gave me a thank you message, even though they knew that I had been using Spreadsheet programs to help solve their puzzles…. This obviously raises many questions.
Regardless of the questions raised, in this video I work through almost the entirety of the Tengri 137 Name calculation BY HAND to show how it is simply playing with patterns of repeating digits in fractions and numbers. I like to call this the divide by “9s” trick!
But the only problem of doing this by hand is that we obtain a road block, namely the last part of the puzzle which requires using Prime Number Factorization of VERY large numbers, namely a 44 digit number I call the Tengri Number, T, and a 46 digit number consisting of all 9s. The problem with this is that is it (near) IMPOSSIBLE to solve this by hand (without luckily guessing), and in fact many online prime factorization calculators can’t even perform over 10 to 15 digit prime factorizations!!! Luckily the amazing Wolfram Alpha calculator can do much larger digits!
Thus the only part of the calculation that I had to rely on a “tool” was the incredibly hard large prime factorization operations. Now here is where I give a counter-challenge to Tengri 137… If Defango is right that we aren’t allowed to use “tools” to solve these puzzles, than how do they expect us to solve the prime factorization calculations by hand?? I challenge them, or anyone for that matter, to show how that is possible, because that type of knowledge might just break the internet….
I may look into further #Tengri137 puzzles because they are very cool, so stay tuned for what I discover!
UPDATE
Typo at 15:25. Prime Factors of 30 = 5x3x2 NOT 15x5x3x2
Download PDF Notes: https://1drv.ms/b/s!As32ynv0LoaIhu9vwn5VlJcLABipPw
View the Full #Tengri137 Series: https://mes.fm/tengri137-playlist
Watch video on:
- 3Speak:
- Odysee: https://odysee.com/@mes:8/tengri137-part-8-mes-cheating:6
- BitChute:
- Rumble:
- DTube:
- YouTube:

View Video Notes Below!
Download these notes: Link is in video description.
View these notes as an article: @mes
Subscribe via email: http://mes.fm/subscribe
Donate! :) https://mes.fm/donate
Buy MES merchandise! https://mes.fm/store
More links: https://linktr.ee/matheasy
Follow my research in real-time on my MES Links Telegram: https://t.me/meslinks
Subscribe to MES Truth: https://mes.fm/truthReuse of my videos:
- Feel free to make use of / re-upload / monetize my videos as long as you provide a link to the original video.
Fight back against censorship:
- Bookmark sites/channels/accounts and check periodically
- Remember to always archive website pages in case they get deleted/changed.
Recommended Books:
- "Where Did the Towers Go?" by Dr. Judy Wood: https://mes.fm/judywoodbook
Join my forums!
- Hive community: created/hive-128780
- Reddit: https://reddit.com/r/AMAZINGMathStuff
- Discord: https://mes.fm/chatroom
Follow along my epic video series:
- #MESScience: https://mes.fm/science-playlist
- #MESExperiments: @mes/list
- #AntiGravity: @mes/series
-- See Part 6 for my Self Appointed PhD and #MESDuality breakthrough concept!- #FreeEnergy: https://mes.fm/freeenergy-playlist
- #PG (YouTube-deleted series): @mes/videos
NOTE #1: If you don't have time to watch this whole video:
- Skip to the end for Summary and Conclusions (if available)
- Play this video at a faster speed.
-- TOP SECRET LIFE HACK: Your brain gets used to faster speed!
-- MES tutorial: @mes/play-videos-at-faster-or-slower-speeds-on-any-website- Download and read video notes.
- Read notes on the Hive blockchain #Hive
- Watch the video in parts.
-- Timestamps of all parts are in the description.Browser extension recommendations:
- Increase video speed: https://mes.fm/videospeed-extension
- Increase video audio: https://mes.fm/volume-extension
- Text to speech: https://mes.fm/speech-extension
--Android app: https://mes.fm/speech-android

Recap on Previous Parts
Part 1: "Magic" Cubes Calculator
Part 2: Odin's Triple Horn: Perfect Squares
Part 3: Odin's Triple Horn: Visual Representation
Part 4: Odin's Triple Horn: AMAZING MES Custom ∑ Calculation!
Part 5: Intergalactic Dance Battle vs. #Tengri137
Part 6: Intergalactic Dance Battle vs. #Tengri137 Round 2: MES Puzzle Challenge
Part 7: Calculation of Tengri's Mathematical Name
Link to Playlist: https://www.youtube.com/playlist?list=PLai3U8-WIK0HUv8mv9gzQc3Ej4csHIQb3
#Tengri137 Part 8: MES Cheating on the Alien Math Exam??
Recall from my last video that I showed how #Tengri137 "Name" Calculation was made and showed how you can make your very own!
Here is the "Name" and the resulting calculation:


But for some very strange reason, Defango did a hit-piece against me…. # WTF

Defango claimed that I "cheated" by using the Wolfram Alpha calculator to solve the whole puzzle…. Which "anyone could have done", and that #Tengri137 said you can't use "Tools"…. So why was I not told about this until Part 7? And why did Tengri give me a Thank You message, knowing that I had used Spreadsheet "Tools" in my earlier videos? # Questions
Regardless of those questions, I will show that it is (near) impossible to solve this Tengri Name calculation "by hand", because of the large number Prime Factorization…
First off, in the calculation that Defango showed in his video, he is wrong in that I used Wolfram Alpha to "solve" the puzzle, but rather I was showing that the "9's pattern" works!
Let's try solving the Tengri Name calculation "by hand":
Let's first establish the following pattern


Note that this works for ANY numerator, assuming it's less than the denominator, not just 1.
This is because each number can by broken up into a sum of fractions:
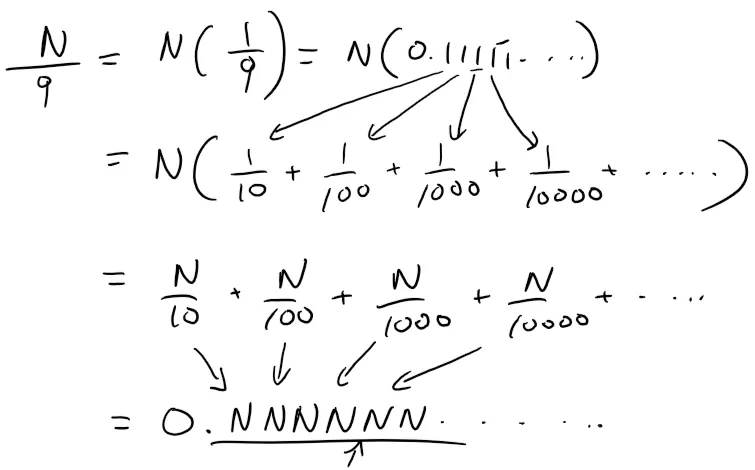
This means that we can write ANY number in a variety of repeating ways, even the exact calculation that #Tengri137 used!!


To make it easier I will call Tengri's repeating non-zero numbers pattern as T.
Since it has a period of 46, we have 46 "9s". That is all.

Now to obtain the Prime Number calculation, we need to perform Prime Number Factorization of the numerator and denominator:
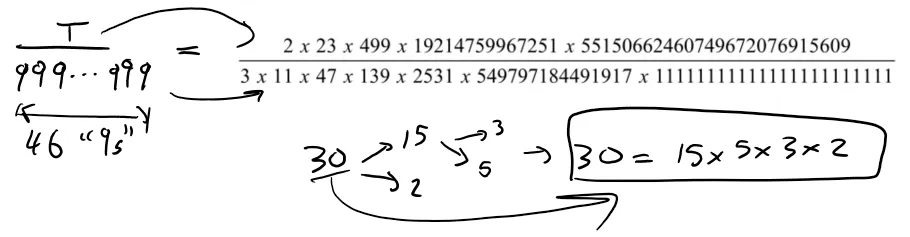
https://en.wikipedia.org/wiki/Integer_factorization
Retrieved: 21 April 2017Integer factorization
In number theory, integer factorization is the decomposition of a composite number into a product of smaller integers. If these integers are further restricted to prime numbers, the process is called prime factorization.
When the numbers are very large, no efficient, non-quantum integer factorization algorithm is known. An effort by several researchers, concluded in 2009, to factor a 232-digit number (RSA-768) utilizing hundreds of machines took two years and the researchers estimated that a 1024-bit RSA modulus would take about a thousand times as long.[1] However, it has not been proven that no efficient algorithm exists. The presumed difficulty of this problem is at the heart of widely used algorithms in cryptography such as RSA. Many areas of mathematics and computer science have been brought to bear on the problem, including elliptic curves, algebraic number theory, and quantum computing.
Thus it is (near) impossible to perform prime factorization of very large numbers by hand, especially 46 digits numbers…
In fact, most calculators online can't even perform such large calculations!

http://www.mathsisfun.com/numbers/prime-factorization-tool.html

Luckily for us, the amazing Wolfram Alpha calculator can do so!! # AMAZING
https://www.wolframalpha.com/input/?i=factor+9999999999999999999999999999999999999999999999
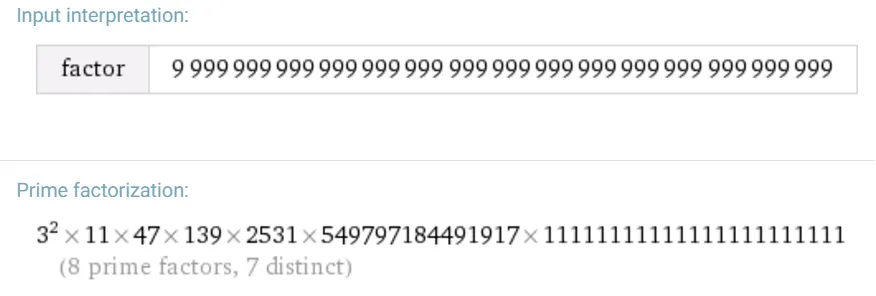
https://www.wolframalpha.com/input/?i=factor+72973525613766677788831415921618033299792458

Thus we have:

This simplifies to the #Tengri137 Name!

Now I would double check my work with Wolfram Alpha but I am worried Defango might take it out of context and say that I'm using too advanced A.I., etc. …. # LOL
https://twitter.com/Higher4Minds/status/855602043985158146
- Higher4Minds

And now my challenge to #Tengri137
How is it possible to perform prime factorization of a 44 or 46 digit number by hand??
Can you please provide us a way??
If you can then you just might be able to break the internet because many security systems rely on the difficulty for computers to perform prime factorization of large numbers…. (albeit larger than the Tengri numbers, but same idea).
I also may look into further #Tengri137 puzzles because I find them very cool so stay tuned for what I discover!
--
View the Full #Tengri137 Series: https://mes.fm/tengri137-playlist
