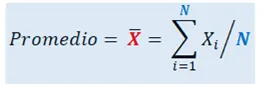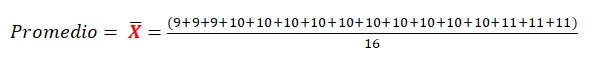En el proceso de aprendizaje de las ciencias matemáticas podemos encontrarnos con datos estadísticos que pueden proporcionar una descripción de una situación real, aproximada o ficticia cuando analizamos ese conjunto de datos, representados por números reales (ℝ). Partamos por el ejemplo clásico de varios alumnos de una clase de quinto grado de educación básica, cuyas edades son: 9, 9, 9, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 11, 11, 11

Valor promedio:

cuando se dispone de un conjunto de datos o valores numéricos y deseamos calcular el valor promedio se procede de la siguiente manera: se suman todos los datos disponibles (X_i) y el resultado se divide entre el número total de datos (N), aplicando la siguiente expresión matemática:

número total de datos: 16
sumatoria de los valores 160
valor promedio: 10

Si realizamos el análisis desde el punto de vista de la Estadística Descriptiva tendríamos una idea que la edad de los estudiantes de este curso de quinto grado debería ser de 10 años, aunque podemos distinguir que existen niños de 9 años y de 11 años. El valor numérico que acabamos de obtener es un número calculado que se aproxima en promedio al valor de las edades de estos estudiantes, y como fue de 10 años, la intuición nos lleva a una descripción que se trata de niños de edades de 10 años.

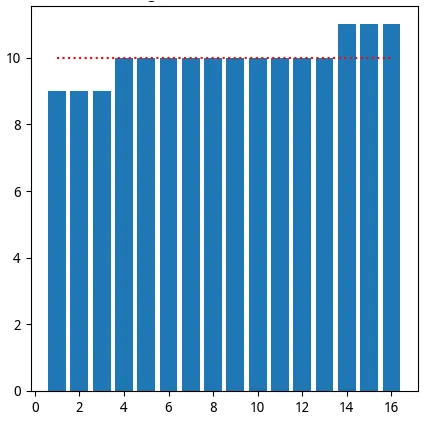
Precisamente, el valor promedio corresponde con el valor de equilibrio entre el peso (valor absoluto) que representa cada dato, y en este ejemplo se acerca a la realidad (perceptiva). Ahora, si consideramos la edad de la Maestra de la clase y su colaboradora, cuyas edades son 50 y 35 años, respectivamente más la asistencia de 3 alumnos, cuyas edades son: 9, 10 y 11 años, ¿cuál es la edad promedio en el salón de clases del quinto grado?

Promedio de edades:

número total de datos: 5

sumatoria de los valores: 115

valor promedio: 23

la balanza se desplaza hacia la derecha, tratando de ubicarse en el punto de equilibrio de los valores numéricos.

El valor promedio de edades es de 23 años (línea roja), pero la estadística descriptiva sugiere que no existe ninguna persona con 23 años en este salón de clases, diríamos que se trata de jóvenes universitarios, lo cual intuitivamente es erróneo. Recordemos que se trata de un valor calculado y no necesariamente corresponde a un valor de datos reales o medidos de forma directa, como preguntarle a una persona realmente.

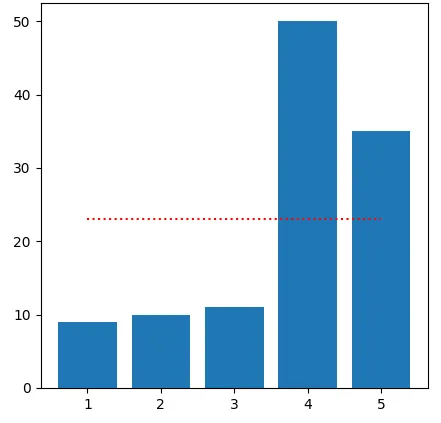
En definitiva, estaremos haciendo una distribución equitativa de los valores numéricos entre las cantidades de datos (valores) representados en una tabla de datos o histograma, es decir, tratar de buscar un equilibrio entre los valores numéricos (repartición).

Apoyo bibliográfico y fuente de imágenes

Nuestras ideas y conocimientos que podamos tener sobre el tema tratado en este artículo pueden ampliarse de manera voluntaria al consultar el siguiente catálogo de referencias:

• Imagen de 777546: Portada de valor promedio
• Wikipedia: Estadística descriptiva
• Blog: Estadística descriptiva
• Artículo: La estadística descriptiva
• Economipedia: Estadística descriptiva

Los cálculos estadísticos
brindan una idea sobre la tendencia,
de un conjunto de datos que aportan información
sobre un hecho en particular