Esta situación de juegos tradicionales me puso a pensar en las esferas de colores que lancé (o dejé caer) en una Tabla de Galton, digo tabla porque literalmente era de madera, aunque en realidad se escucha mejor llamarla la

Máquina de Galton

y en la cual no sabía a ciencia cierta cuál era la trayectoria que recorrería cada esfera.

Estas experiencias de distribución normal me apasionan porque se tienen varios caminos, opciones o posibilidades de que en un lanzamiento de un dado salga un 4, o ver cuántas esferas llegan a caer en las 9 casillas que se presentan en la máquina de Galton que vemos en la portada de esta publicación.

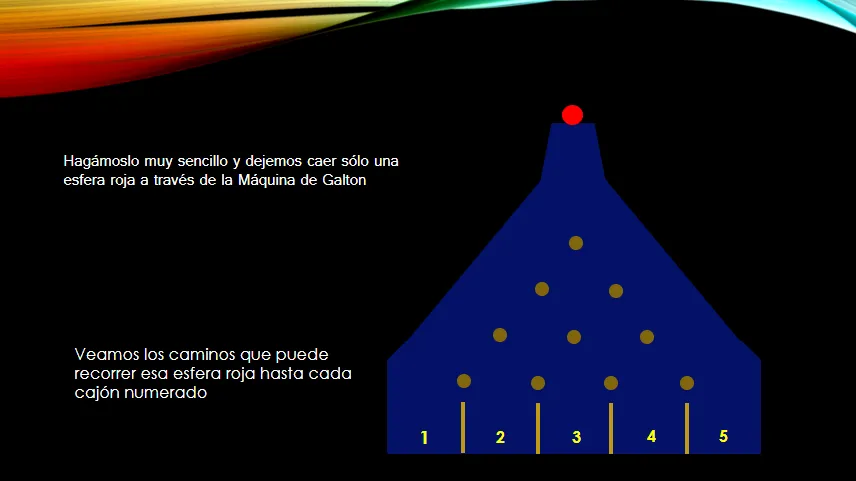
Este es un ejercicio que podemos resolverlo de forma directa y mentalmente nos imaginamos el recorrido de la esfera roja por el borde derecho y llegará a la casilla número 5, mientras que si baja por el borde izquierdo de la máquina de Galton, llegará directamente al lugar número 1. Estos son los caminos más directos luego de rozar levemente el primer obstáculo.

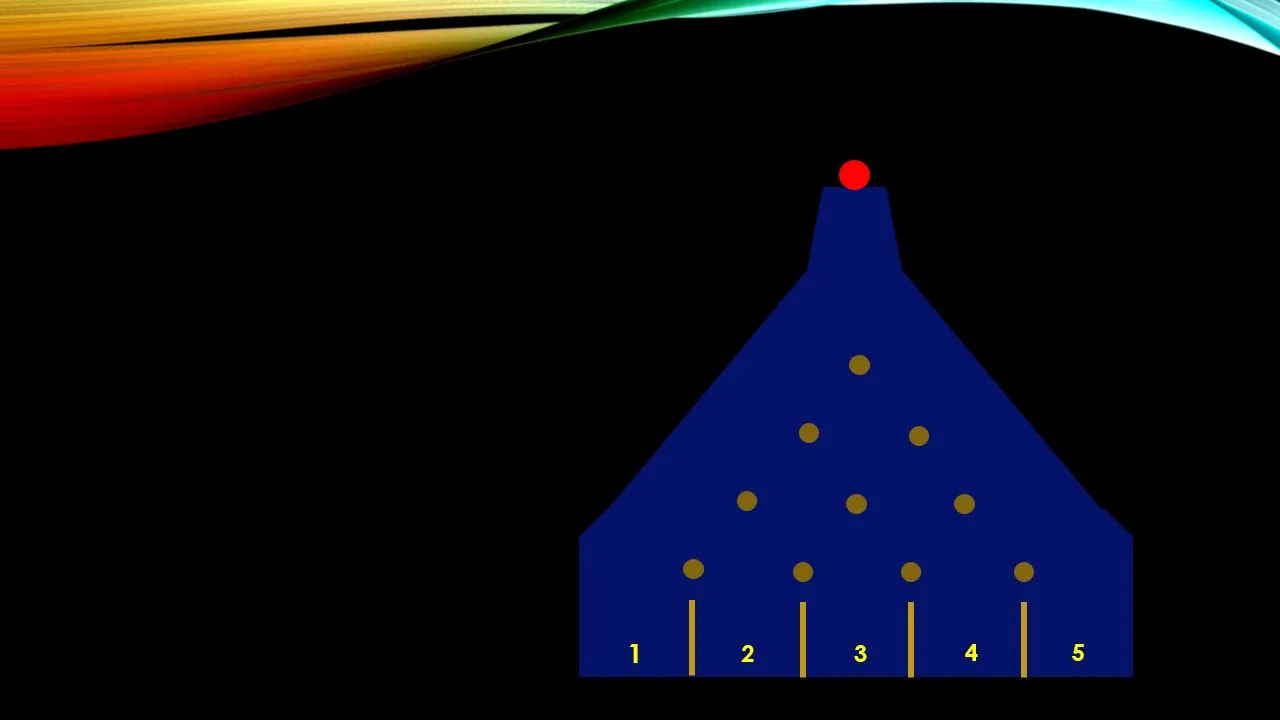
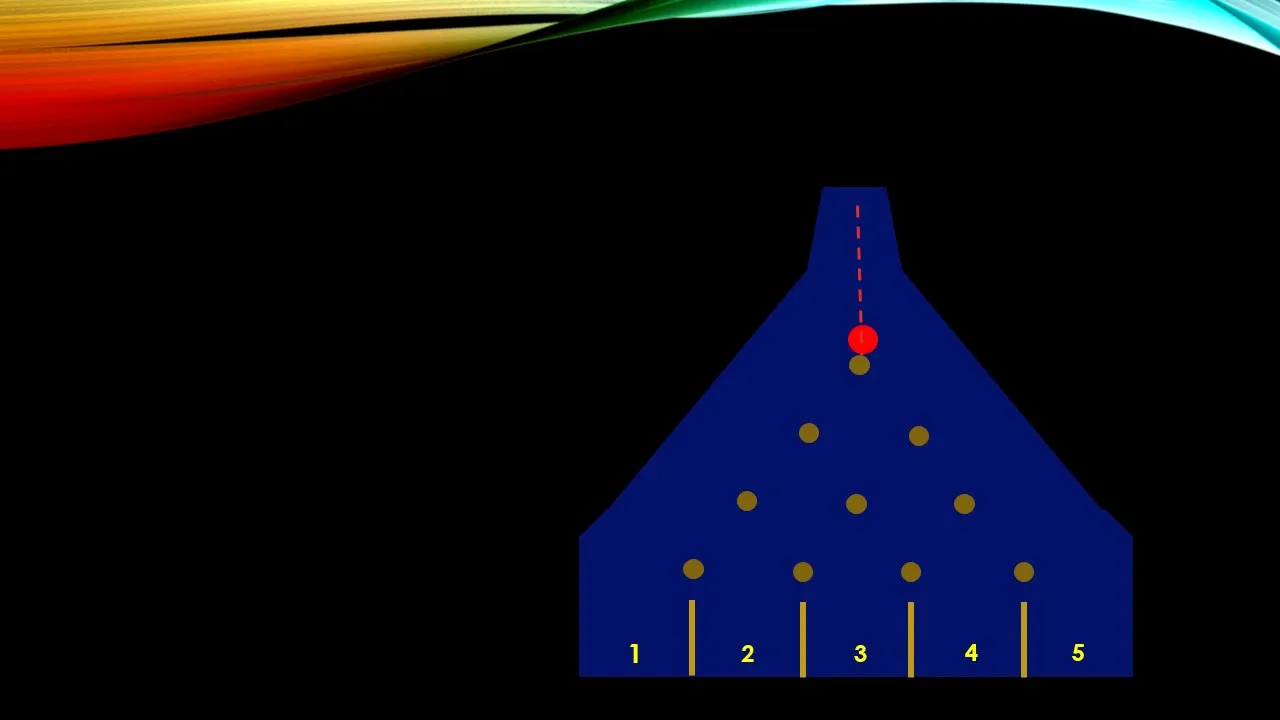
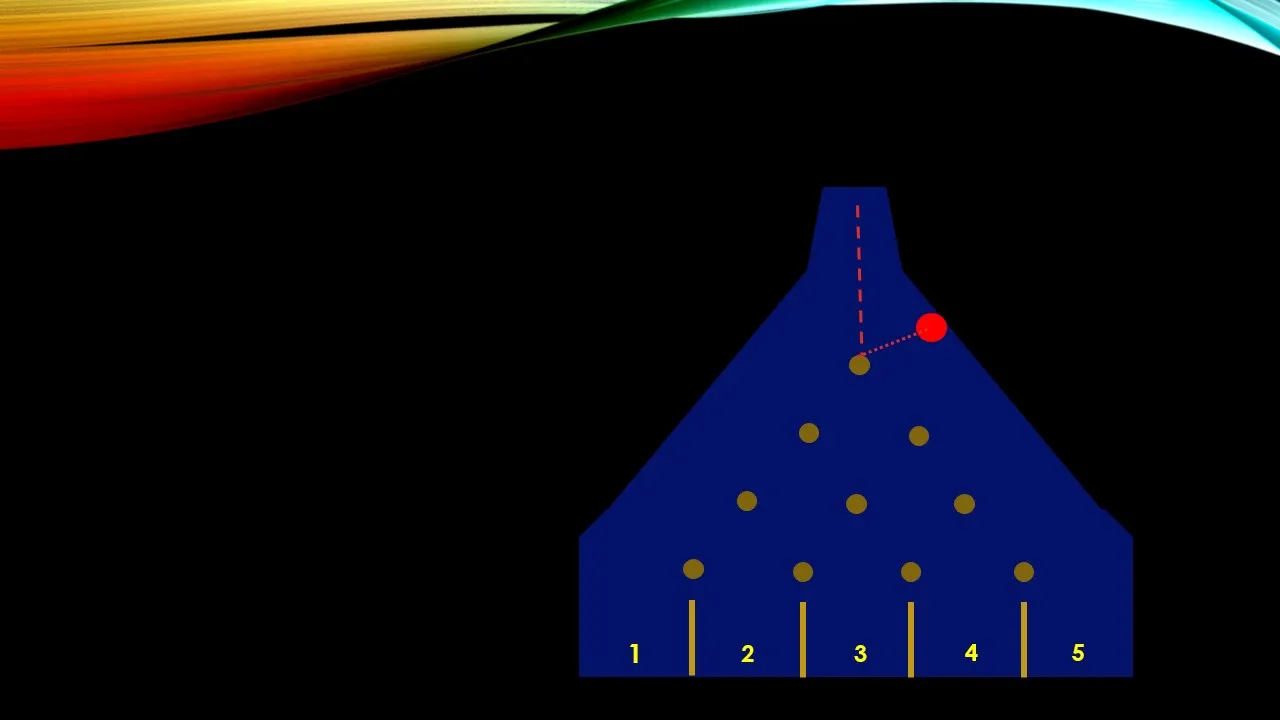
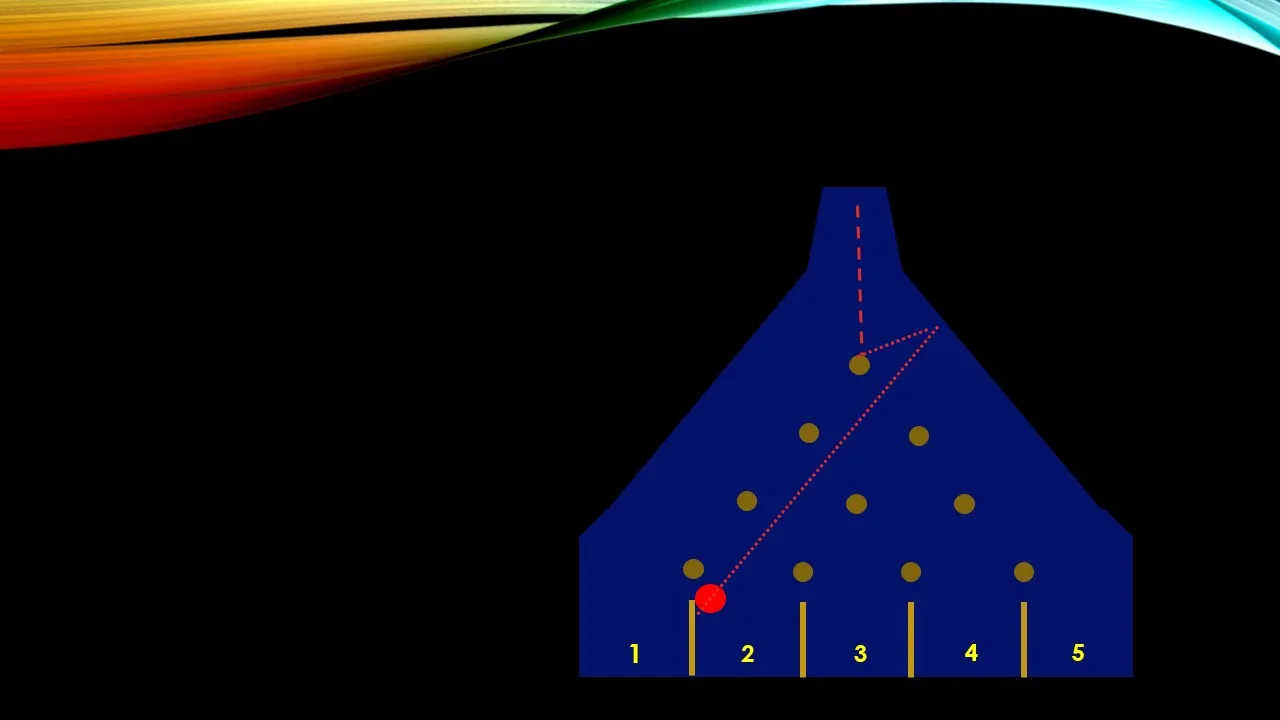
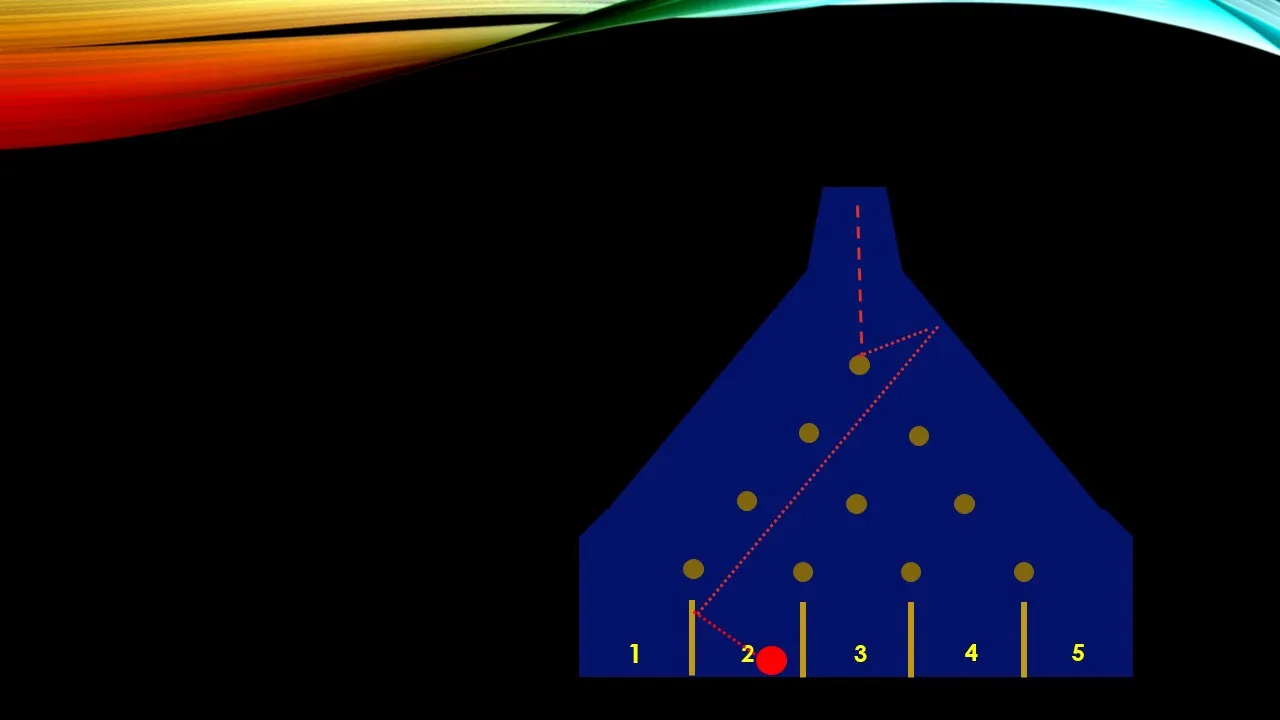
De esta manera he simulado los choques de la esfera roja con los obstáculos y paredes de la máquina de Galton, por una tercera vía posible y vemos que va a parar en la casilla número 2. En la siguiente imagen les presentaré otras 3 posibilidades de caer en esa casilla:

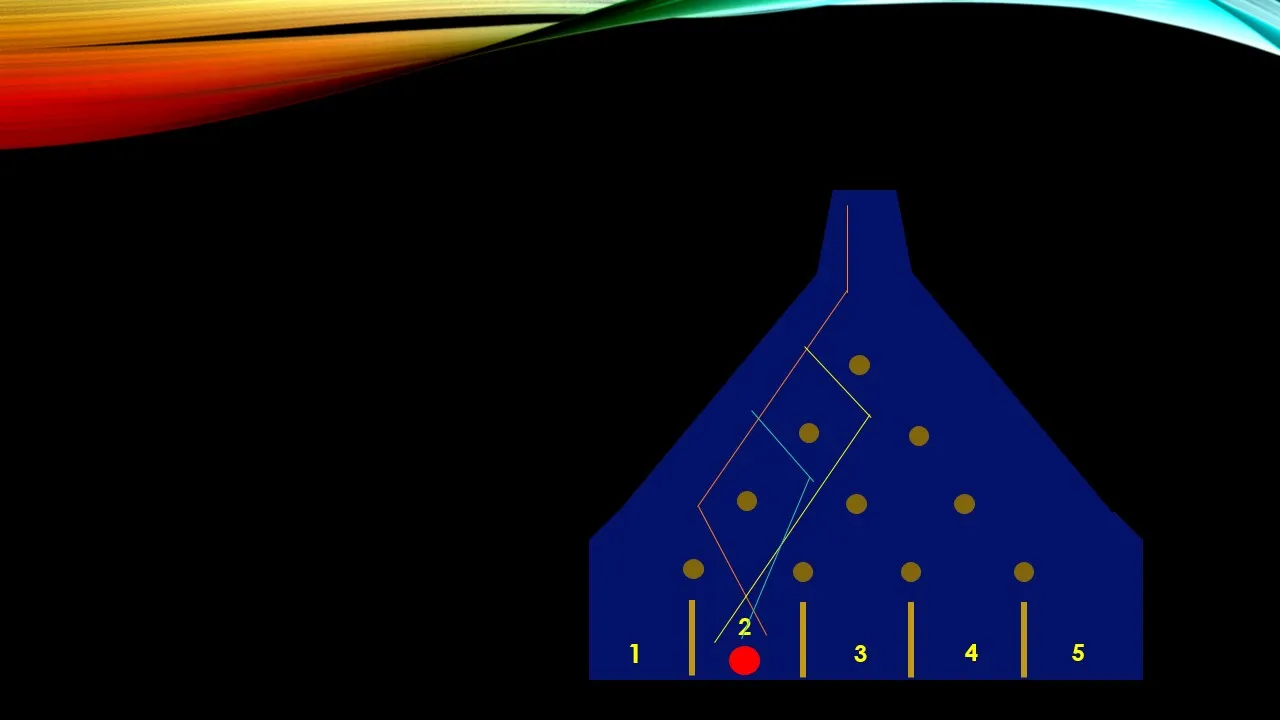
Cuando la esfera toma el rumbo por el borde izquierdo, existe una alta probabilidad que caiga en la casilla 1, 2, 3 y 4, mientras que es menos probable (o imposible) que se dirija a la casilla 5. En una sección a continuación haré los cálculos de las probabilidades en esta distribución aleatoria.

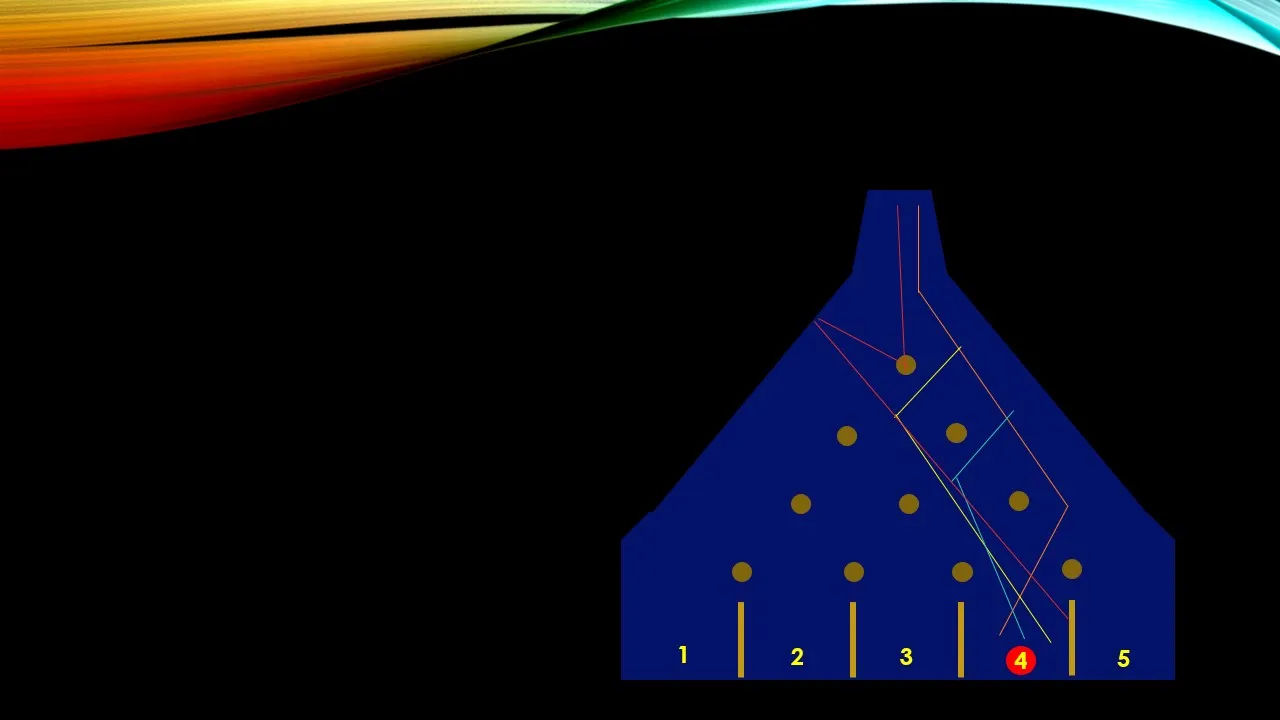
Se me complicó el trazado de líneas para la casilla 3, porque se entrelazaban las líneas, así que puede quedar como asignación personal. Sin embargo, las opciones son 6, 3 que van rumbo por el lado derecho y 3 por el borde izquierdo, los cuales se dirigen hacia la zona central, casilla número 3.

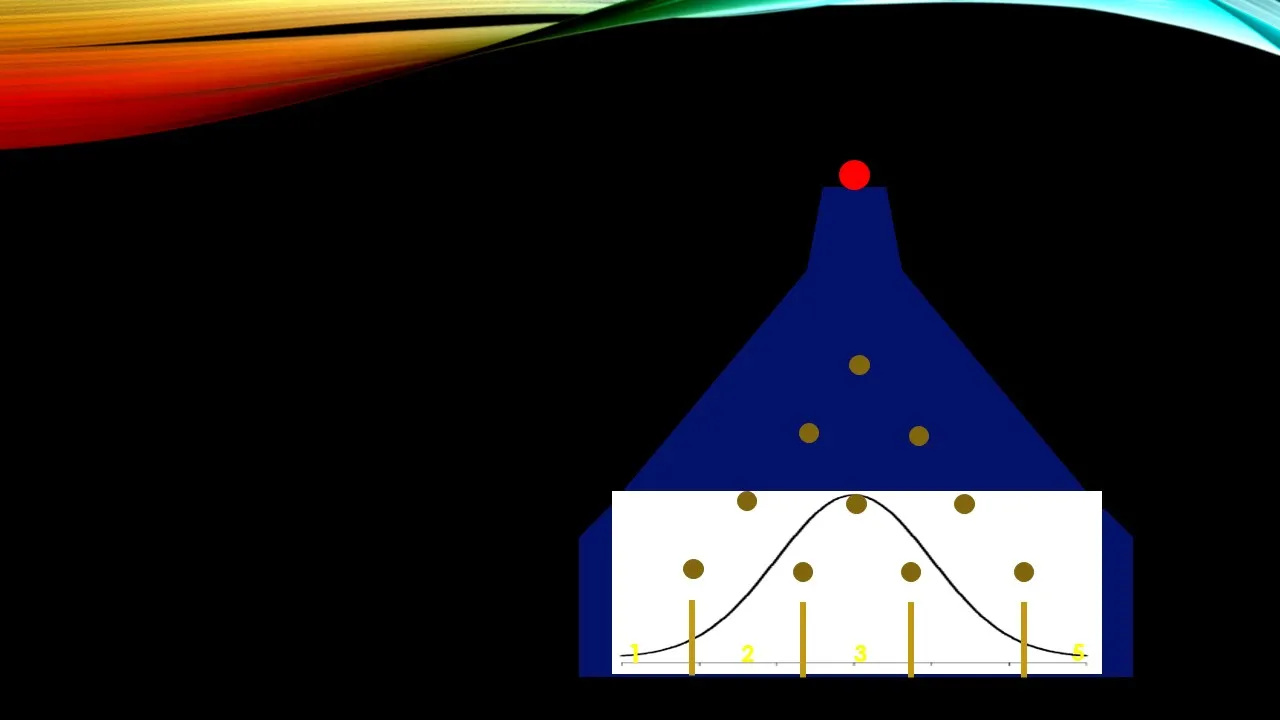
Como tenemos un total de 16 opciones de rutas diferentes por las que puede desplazarse la esfera roja, entonces podemos calcular las probabilidades de cada evento, es decir, la probabilidad que la esfera caiga en la casilla 1, será:

Como les mostré en la otras imágenes, las rutas aleatorias para la casilla 2 fueron 4, por lo que la probabilidad sería:

Indudablemente, la mayor cantidad de probabilidad según la distribución normal que anexé en la figura anterior recae en la casilla número 3

Repasando este ejemplo, me he dado cuenta que la

Máquina de Galton

y el análisis de las probabilidades guarda relación con el donde la quinta fila se corresponde con las 5 casillas de la máquina de Galton y el número representa los posibles caminos (PC) para llegar a esas casillas: PC[1] = 1 PC[2] = 4 PC[3] = 6 PC[4] = 4 PC[5] = 1

Una de las congruencias Matemáticas por las que me apasiona compartir estos temas en la comunidad HIVE.

Apoyo bibliográfico y fuente de imágenes

Nuestras ideas y conocimientos que podamos tener sobre el tema tratado en este artículo pueden ampliarse de manera voluntaria al consultar el siguiente catálogo de referencias:

• Imagen de Antoine Taveneaux: Portada: Distribución aleatoria
• Wikipedia: Distribución normal
• Wikipedia: Máquina de Galton
• Wikipedia: Triángulo de Pascal
• Imagen de Drini: Figura del triángulo de Pascal