La aplicación de las Matemáticas en la delimitación de terrenos, planos de construcción, ingeniería civil, etc, ha sido una herramienta útil para desarrollar cualquier tipo de proyecto de obras civiles. La determinación del área de un terreno o el perímetro de una construcción se inicia con la geometría básica, necesitando saber la longitud o valor numérico de la base, altura, los lados, diagonal y hasta ángulos de determinados parámetros para hallar el perímetro, área o volumen de un espacio unidimensional, bidimensional u objeto tridimensional, respectivamente.
Me resultó fácil el uso de Geogebra para hacer más rápido el proceso de enseñanza-aprendizaje de los temas matemáticos que muchas veces resultan tan complicados para el que se inicia en esta área del conocimiento, pero que debemos hacerlos ver como un proceso sencillo a través de las Matemáticas sin secretos.

Supongamos que tenemos una figura geométrica cuadrada, cada lado mide 4 cm. Hallar el perímetro del cuadrado y el área de esta figura.
Me parece ideal si comenzamos a resolver desde la perspectiva del espacio 1D, 2D y 3D, progresivamente para ir acostumbrando nuestro cerebro a resolver situaciones básicas hacia lo más complejo.
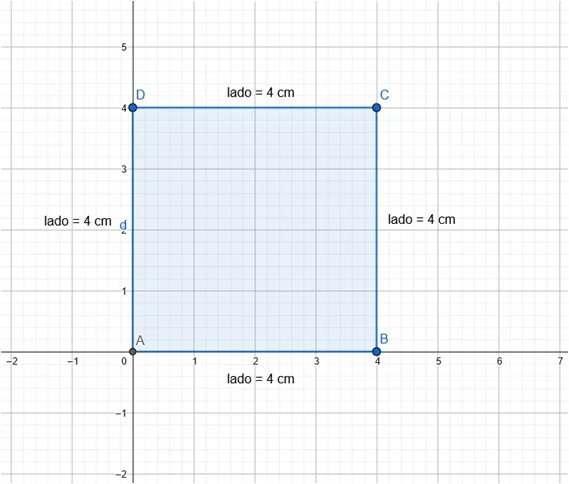
El perímetro está determinado por la longitud de todos los lados, esto es sumar los 4 lados (iguales) en este cuadrado:
lado 1 = 4 cm
lado 2 = 4 cm
lado 3 = 4 cm
lado 4 = 4 cm
Perímetro
= 16 cm
La suma de sus lados unidimensionales debe dar como resultado una unidad de medida métrica unidimensional, esto es "centímetros"
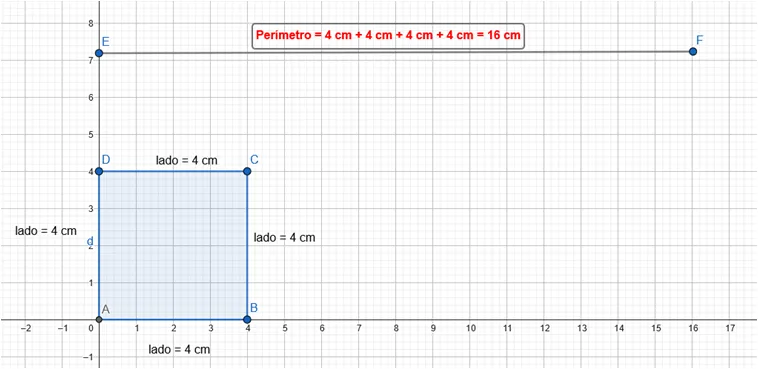
Para calcular el área de un cuadrado es muy fácil, se introduce el concepto de la base (donde se apoya la figura geométrica) y la altura desde la base hasta la sección más alta que pueda llegar. También se usa equivalentemente el concepto de lado y en el caso de un cuadrado estos resultan ser iguales, los 4 lados.
Así que el
área de un cuadrado
es el producto de la base (lado = 4 cm) por la altura (lado = 4 cm)
A▉ = base × altura
A▉ = 4 cm × 4 cm
A▉ = 16 cm2
¿Siempre van a ser iguales el Perímetro = 16 cm y el Área = 16 cm
2?
La respuesta definitiva es NO, este caso es especial en el cual el valor numérico es "16", pero ni las unidades son iguales por tratarse de parámetros diferentes.
Otra figura geométrica o espacio dimensional es el caso de un rectángulo de base = 8 cm y la altura = 4 cm. Note que ya no estoy hablando de lados, como en el caso de un cuadrado que todos los lados son iguales (lado = 4 cm), ya que aquí se marca una diferencia notable entre las longitudes y sus valores numéricos son diferentes.

Para calcular el perímetro de este rectangulo vamos a sumar cada una de las longitudes de sus 4 lados, ya sabemos que 2 de ellas son iguales por la base y las otras 2 son iguales por su altura.
Perímetro = 8 cm + 4 cm + 8 cm + 4 cm = 24 cm
El
área de un rectángulo
es el producto de la base = 8 cm por la altura = 4 cm
A▅ = base × altura
A▅ = 8 cm × 4 cm
A▅ = 32 cm2
Perímetro y área de un triángulo
El área de un cuadrado ya lo había resuelto usando el concepto de un
binomio, ahora con un triángulo la situación es diferente y vamos a ver el caso de que esté envuelto dentro de un cuadrado o rectángulo.
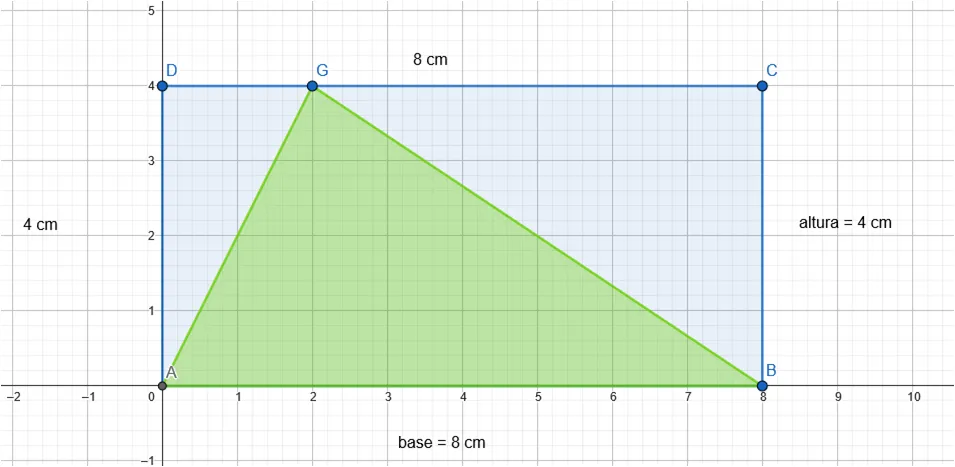
El triángulo AGB de la figura anterior tiene las siguientes longitudes: en su base 8 cm (lado AB), su altura 4 cm (desde la base hasta el punto más alto en G), el lado AG = 4,5 cm (segmento [A,G]) y el lado GB = 7,2 cm (segmento [G,B]).
Note que la sumatoria de los 3 lados del triángulo va a dar como resultado el perímetro del triángulo, así que:
Perímetro = 8 cm + 7,2 cm + 4,5 cm = 19,7 cm
Calculado el perímetro, sin mucho trauma para el estudiante y sin ninguna complicación a través de una suma aritmética.
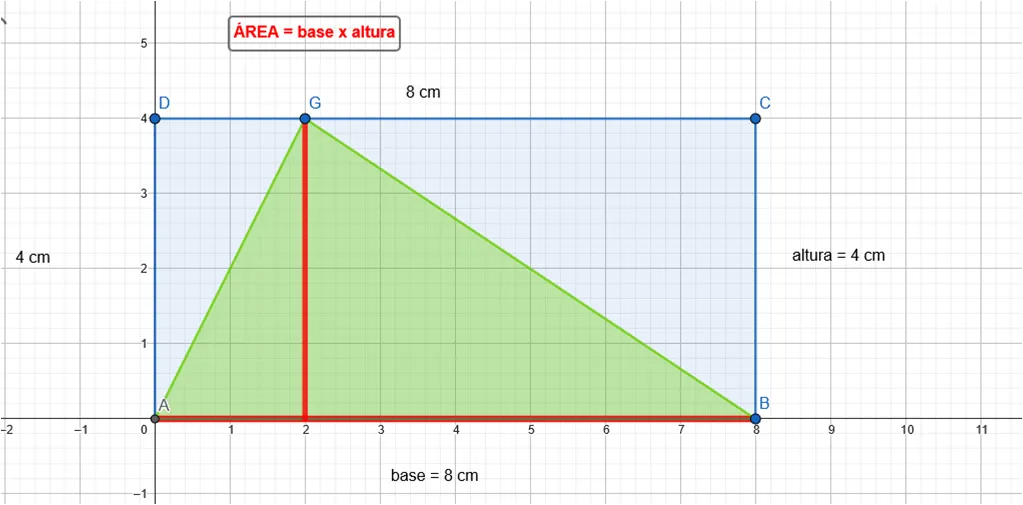
El
área de un triángulo
es el producto de la base = 8 cm por la altura = 4 cm y lo dividimos entre 2:
A▲ = (base × altura)/2
A▲ = (8 cm × 4 cm)/2
A▲ = 16 cm2
¿Será una curiosidad matemática que haya aparecido nuevamente el 16, o existe una relación entre los cálculos realizados en estas figuras geométricas?
Para el cálculo del área de un cuadrado, un rectángulo y un triángulo lo común es la base multiplicada por la altura
, claro que para el triángulo se divide entre 2. Entonces, la lógica matemática nos da para pensar en que podemos
envolver al triángulo con un rectángulo de base y altura igual que la del triángulo, además el área del triángulo debe ocupar la mitad del área del rectángulo. Numéricamente:
A▅ = 32 cm2
A▲ = (A▅)/2
A▲ = 16 cm2
Gráficamente, dividimos el rectángulo (azul) por la mitad, designando el segmento HI:
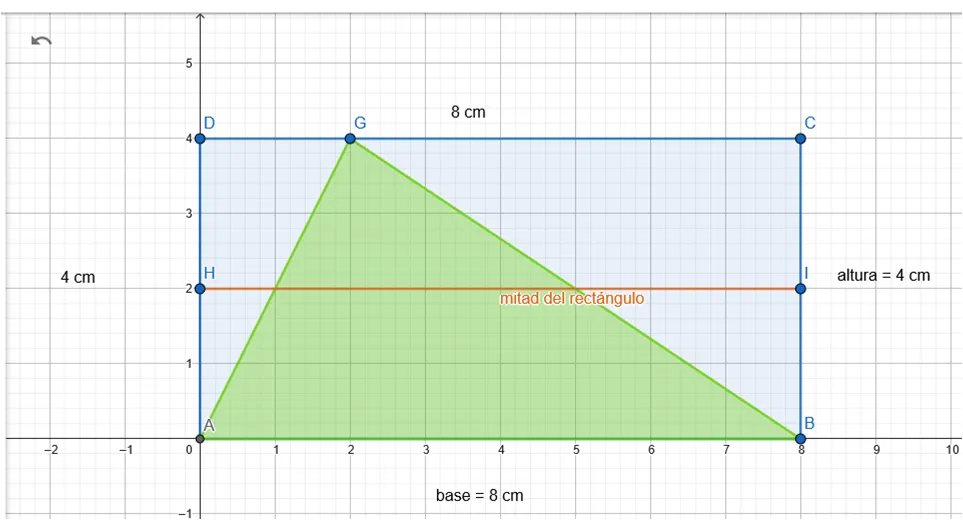
Trazamos una línea perpendicular al segmento HI hasta el punto G del triángulo (segmento GJ):
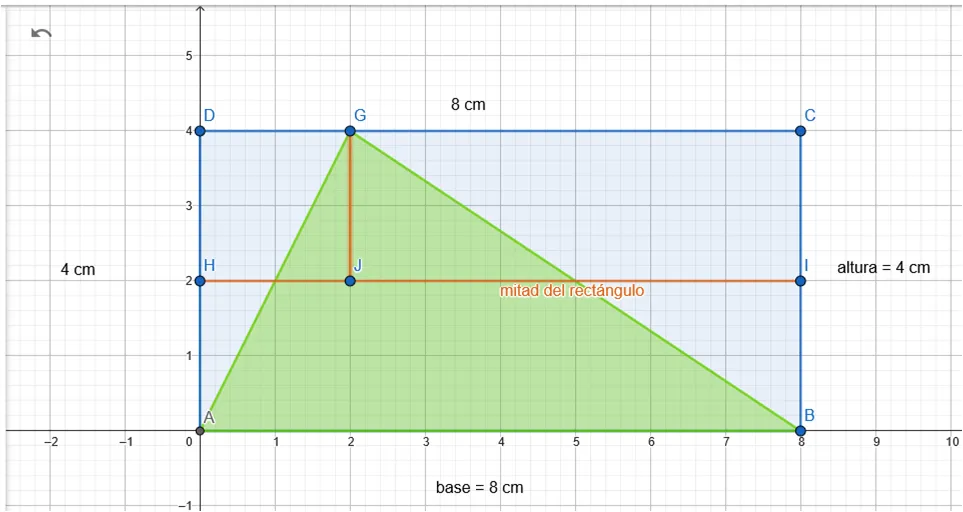
Resulta 1 triángulo GJKa la izquierda:
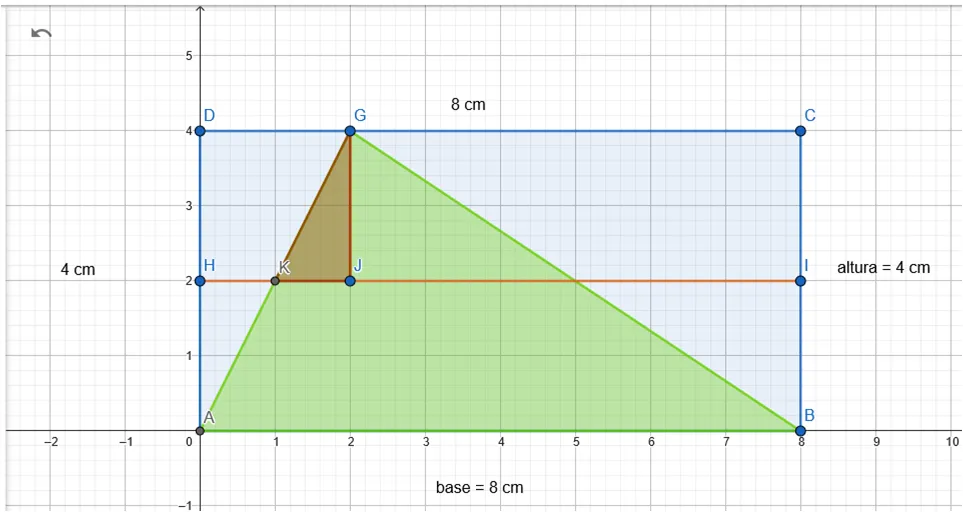
También otro triángulo GJL a la derecha:
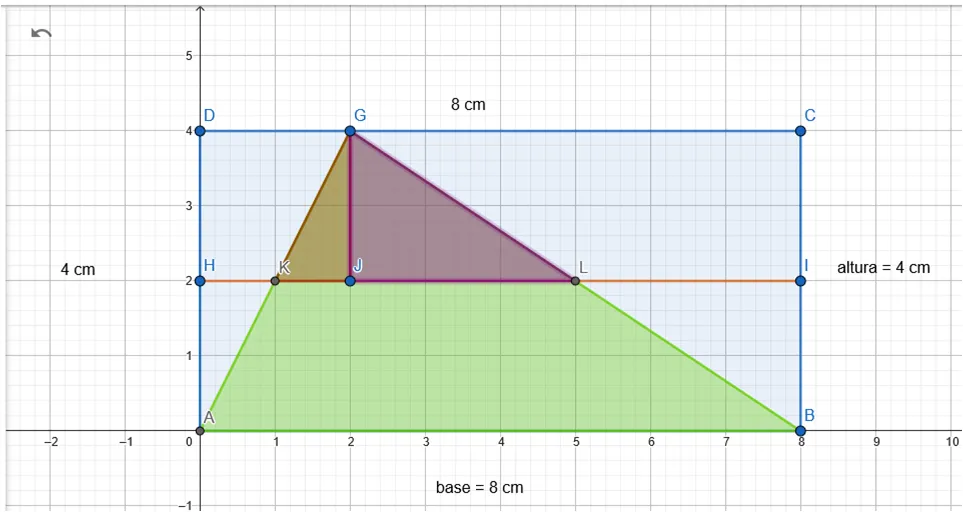
Estos 2 triángulos que ocupan la parte superior del triángulo original, también están distribuidos en la mitad superior del rectángulo, caben perfectamente en los espacios vacíos de la mitad inferior del rectángulo.
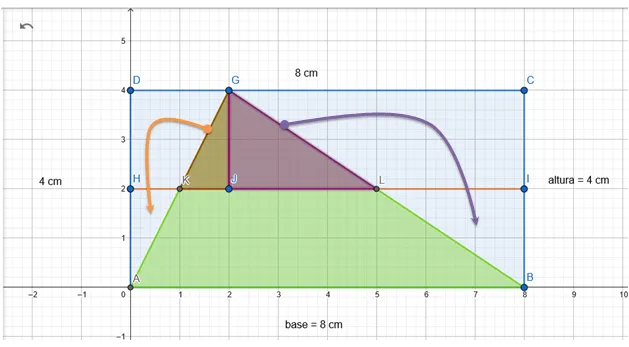
Es notable que al redistribuir estas secciones triangulares hacia la mitad inferior del rectángulo, vamos a ocupar completamente esta sección del rectángulo y se cumple la relación:
A▲ = (A▅)/2
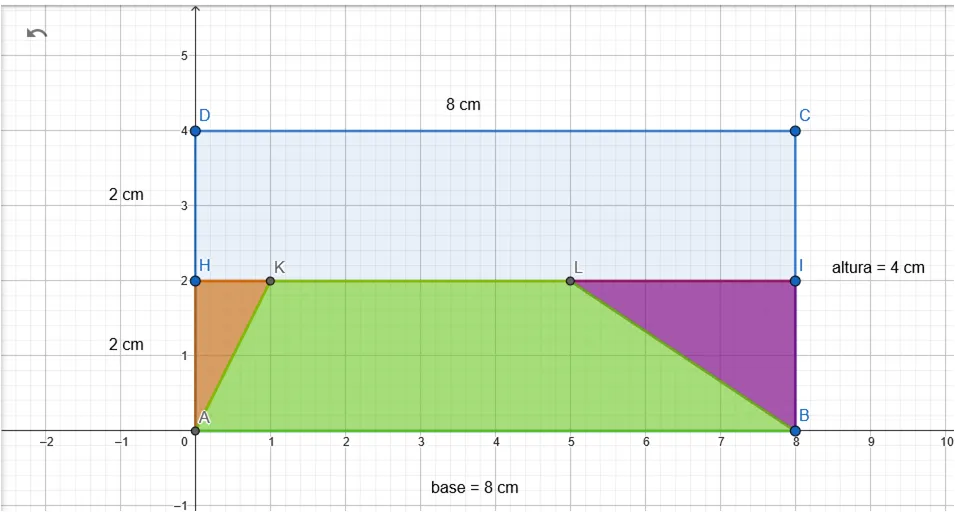 Finalmente llegamos a la demostración gráfica que el área de un triángulo es igual a la mitad del área de un rectángulo.
Finalmente llegamos a la demostración gráfica que el área de un triángulo es igual a la mitad del área de un rectángulo.
Apoyo bibliográfico y fuente de imágenes
Nuestra lógica y razonamiento matemático pueden ampliarse de manera voluntaria al consultar el siguiente catálogo de referencias:
Las identidades matemáticas son expresiones algebraicas
que facilitan el cálculo de magnitudes susceptibles
a ser medidas, como el área de un terreno o una figura geométrica











