
(Todas las imágenes y GIF's fueron hechos por mi usando el software matemático GeoGebra Classic 5.)
Las ondas se encuentran presentes en cada momento de nuestro día y quizás ni pensamos en ello, se forman cuando hablamos como ondas sonoras, cuando cae una gota de agua en un estanque, nos permiten comunicarnos a través de nuestro teléfono celular y entretenernos escuchando la radio, realmente estamos inmersos en ellas; estas están íntimamente involucradas con el fenómeno de oscilación y las ondas mecánicas las cuales trataremos a continuación con el movimiento armónico simple por lo cual empezaremos describiéndolo para así adentrarnos en las ondas mecánicas.
Para describir el moviendo armónico simple es necesario que expresemos el desplazamiento del cuerpo en función del tiempo, aquí la aceleración no es constante ya que la fuerza es proporcional al desplazamiento sin embargo podemos encontrar una relación entre el movimiento circular uniforme y el armónico simple.
(Todas las imágenes y GIF's fueron hechos por mi usando el software matemático GeoGebra Classic 5.)
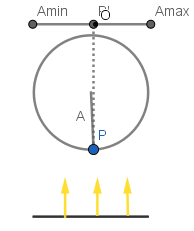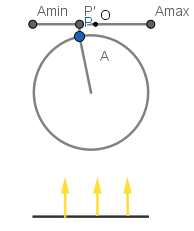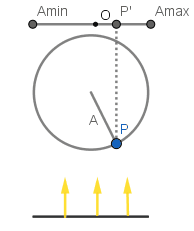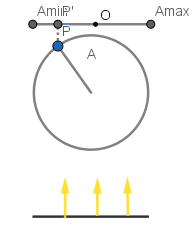
En el GIF podemos ver un punto girando con frecuencia angular constante sobre un círculo de radio A, al ser la frecuencia angular constante el punto describe un movimiento circular uniforme. Se hace incidir luz sobre el punto de modo que este proyecta su sombra y como podemos ver la sombra del punto oscila en movimiento armónico simple mientras el punto se mueve sobre el círculo.
Podemos representar lo anterior de la siguiente forma:

Cómo podemos ver la componente x del vector OP es la componente del punto P y por lo tanto también lo es para la proyección del punto P.
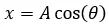
Sin embargo aún nos falta conseguir el desplazamiento en función del tiempo, mientras P gira en el círculo el vector OP también lo hace con la misma frecuencia angular, entonces consideraremos que si el vector OP en un tiempo t = 0 forma un ángulo φ con el eje x entonces en cualquier tiempo t el ángulo θ vendrá dado por:
 (1)
(1)

Una onda mecánica es aquella perturbación que necesita un medio por el cual propagarse, al hacerlo las partículas que forman el medio sufren desplazamientos pudiendo originar deformaciones en el material o sustancia por la cual se propaga, la mínima perturbación producida recibe el nombre de pulso y una secuencia de pulsos realizados periódicamente originan un tren de ondas lo cual resulta en una onda periódica.
Ejemplo de un pulso.
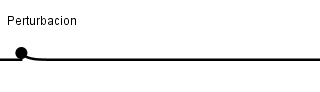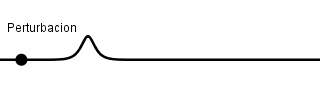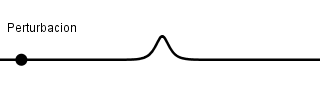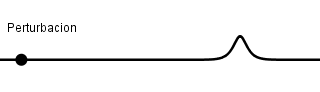
Dependiendo del desplazamiento que realicen las partículas que forman el medio respecto al sentido de propagación de la onda podemos tener dos tipos de ondas:
Longitudinal: cuando el movimiento de las partículas es en la misma dirección en la cual se propaga la onda esta recibe el nombre de onda longitudinal
Transversal: si el movimiento de las partículas es perpendicular al sentido de propagación de la onda esta recibe el nombre de onda transversal.
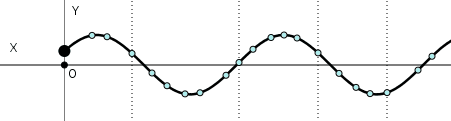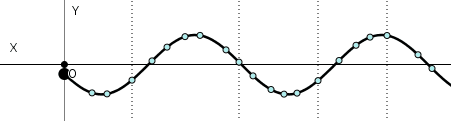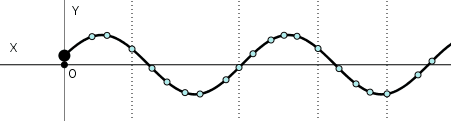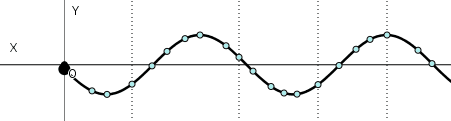
Si la perturbación en el medio se realiza de forma repetitiva es decir, periódica y las partículas que lo conforman describen un movimiento armónico simple la onda que generamos es periódica y toma el nombre de onda senoidal, este tipo de onda es la más sencilla y es sobre la cual realizaremos nuestro estudio, cabe destacar que cualquier onda periódica puede ser vista como un conjunto de ondas senoidales lo cual es de gran ayuda.
Ejemplo onda periódica / tren de ondas.

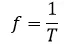
Vemos que la frecuencia es inversamente proporcional al periodo lo que se traduce en que mientras mayor sea el número de repeticiones del patrón (frecuencia) el tiempo (periodo) entre una repetición y otra es menor, de igual forma mientras menor sea la frecuencia mayor es el tiempo que tarda en repetirse el patrón
A pesar de conocer la longitud de onda, amplitud, periodo y frecuencia de una onda para tener una descripción completa de esta es necesario conocer detalladamente el comportamiento de las partículas del medio por el cual la onda se propaga, para ello se recurre al concepto de función de onda una función que nos dice la posición respecto al punto de equilibrio en cualquier instante de tiempo de cualquier partícula que conforma el medio, suponiendo que tenemos una onda transversal y las partículas se mueven perpendiculares al eje x la función de onda es y = (x,t) es decir, depende de la posición en x y el tiempo, describiendo asi el movimiento ondulatorio.
Construcción de la función de onda para una onda senoidal.
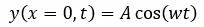 (2)
(2)

Siendo v la velocidad de propagación de la onda, el movimiento del punto x en un tiempo t es el mismo que el del punto x = 0 en un tiempo anterior dado por:

Por lo cual al sustituir lo anterior en la ecuación (2) obtenemos:
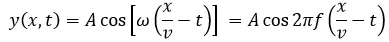
 (3)
(3)
Si ahora definimos una cantidad llamada
 siendo el número de veces que vibra una onda por unidad de distancia y recordando que la frecuencia es igual a
siendo el número de veces que vibra una onda por unidad de distancia y recordando que la frecuencia es igual a 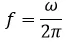 al sustituir en
al sustituir en 
En el caso de una onda que viaja hacia -x el tiempo viene dado por:
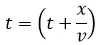
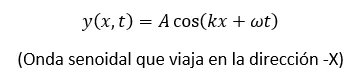
De la función de onda podemos obtener muchísima información sobre lo que está ocurriendo, si realizamos las primera y segunda derivada parcial de la función de onda respecto al tiempo podemos saber la velocidad y aceleración de las partículas, esto es:
Primera derivada parcial respecto al tiempo: velocidad.

Segunda derivada parcial respecto al tiempo: aceleración.
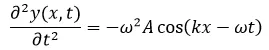
Podemos seguir extrayendo más información esta vez sobre la cuerda si realizamos la primera y segunda derivada parcial respecto a x.
Primera derivada parcial respecto a x: pendiente de la cuerda en cualquier punto.

Segunda derivada parcial respecto a x: curvatura de la cuerda.

Interferencia de ondas.
Hasta ahora hemos analizado una onda que viaja sin nada que le impida que se propague, pero ¿que pasaría si mientras la onda viaja se encuentra con otra y estas "chocan"? Cuando esto sucede las ondas se "unen" y forman una única nueva onda que surge de la combinación de ellas, este fenómeno se conoce como interferencia y es el cual analizaremos a continuación.
Principio de superposición.
Este principio nos dice que, cuando las ecuaciones que rigen el comportamiento de un problema físico son lineales podemos obtener una solución como la suma de los fenómenos que en el intervienen, en el caso que nos interesa si tenemos dos o mas ondas que chocan la onda resultante es simplemente la suma de todas estas.
Consideraremos dos ondas y' e y'' con la misma amplitud y frecuencia pero con distinta fase, si aplicamos el principio de superposición:
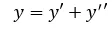
Tenemos que:

Entonces:

Sabiendo que:

Al realizar las operaciones correspondientes:

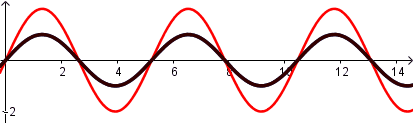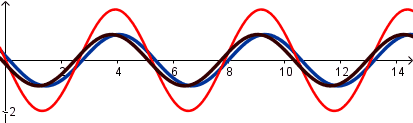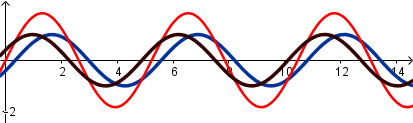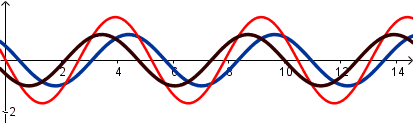
Al sustituir obtenemos:



Simulación interferencia de ondas.
Conclusiones generales:
El movimiento armónico simple se puede obtener como una proyección del movimiento circular uniforme.
Un pulso es la mínima perturbación que se puede dar.
Una secuencia periódica de pulsos origina una onda senoidal.
Las partículas del medio por donde se propaga una onda senoidal describen un movimiento armónico simple.
La características de una onda son amplitud, longitud de onda, frecuencia y una fase del movimiento.
El número de veces que vibra una cuerda por unidad de distancia se conoce como número de onda.
La onda transporta energía y no materia.
La primera y segunda derivada parcial respecto al tiempo de la función de onda nos dan más información sobre el comportamiento de las partículas del medio.
La primera y segunda derivada parcial respecto a x nos dan información sobre la cuerda.
Si la amplitud de la onda resultante debido a la interferencia de ondas es mayor que la amplitud de las ondas que la originan la interferencia es constructiva, si es menor es destructiva.

Espero les haya gustado este tema si así fue estén atentos a mis próximas publicaciones.
(Todas las imágenes y GIF's fueron hechos por mi usando el software matemático GeoGebra Classic 5.)
Material consultado:
Resnick, Halliday y Krane (1993), Física. 3ra edición Compañía Editorial Continental México Volumen 1.
Young, H. D, & Freedman, R. A. FISICA UNIVERSITARIA, volume 1. Pearson Educación de México, S.A. de C.V., 2009.
Tippens, P. E. FISICA - CONCEPTOS Y APLICACIONES. McGrawHill/Interamericana Editores, S.A. DE C.V., 7ma edition, 2001.