En esta publicación quiero hablerles de un trabajo en el que participé y que actualmente he retomado para darle a los estudiantes temas para sus trabajos de grado.
Simulación de la Degradación no oxidativa de Polietileno:
El proceso de degradación de los polímeros es un tópico de gran interés ya que implica la perdida de la mayoría de las propiedades que los hacen útiles. Generalmente se quiere preservar las propiedades de los polímeros agregándole aditivos antioxidantes que eviten el envejecimiento. Sin embargo, el uso masivo de los plásticos se ha convertido en un tema controversial por el daño que se le está causando al ambiente
Un polímero es una cadena muy larga de unidades repetitivas llamadas monómeros (etileno, en nuestro caso). Los monómeros se unen a cientos o miles de otros monómeros mediante enlaces generalmente covalentes.
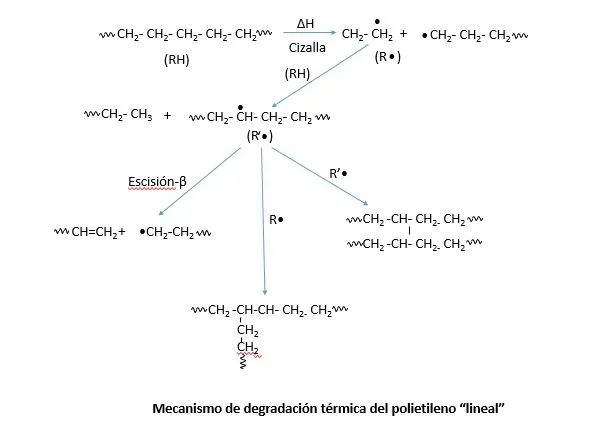
La degradación no oxidativa de un polímero ocurre cuando, debido a la luz, calor o procesos mecánicos, se producen rupturas de las cadenas poliméricas que producen subcadenas de menor peso molecular. El proceso se esquematiza en la figura 1. Se muestra como una cadena de polietileno se rompe en dos subcadenas (llamémoslas x y y) que quedan como radicales libres. Cada uno de ellos puede abstraer un átomo de hidrógeno de otra cadena, pueden formar una insatauración o unirse a otro radical libre para formar cadenas entrecruzadas o ramificadas.
Realicé algunos trabajos de investigación en el tema desde algunos puntos de vista: la degradación del polímero produce radicales libres que son detectados por técnicas experimentales como: Resonancia Magnética Electrónica o por espectrometría infrarroja de transformada de Fourier ya que los fotones absorbidos en la ruptura de las cadenas está en el rango del infrarrojo . Sin embargo, me pareció interesante simular el proceso MonteCarlo usando un método que había sido usado para simular transiciones de fases magnéticas en vidrios de spin y en aleaciones binarias sometidas a procesos térmicos.
Se utiliza una metodología semejante a la que plantee en el artículo https://steemit.com/stem-espanol/@emily61/proceso-de-precipitacion-multifase-modelos-fenomenologicos-simulacion-monte-carlo-y-comparacion-experimental-mediante-medidas-de mediante un programa elaborado en FORTRAN 77. Dado que este proceso es estocástico y que involucra sistemas de ecuaciones diferenciales (de difícil resolución analítica o numérica) es muy conveniente de ser abordado con el Método MonteCarlo.
En este caso, se definieron siete pseudospines u operadores de ocupación:
0: sitio vacio
1: =C=
2: -CH
3: -CH2
4: -CH3
5: =CH2
6: -CH- de entrecruzamiento
7: -CH2 de ramificación
Estos operadores son utilizados para llenar una matriz NxMx2, donde N representa el número de unidades repetitivas (equivalente a los monómeros) y M el número inicial de cadenas poliméricas que se han supuesto iguales.
El proceso podría describirse como sigue:
En cada iteración de la simulación se escoge aleatoriamente una cadena y un sitio donde se romperá y se toma una variable aleatoria ξ que denominamos variable de sorteo. Se define una razón de formación de reacciones donde se forman dobles enlaces y donde ocurren entrecruzamientos (razón doble enlaces/entrecruzamiento) que se denomina OP.
Si la variable de sorteo es mayor que OP se abstrae un átomo de hidrógeno, comenzando una búsqueda aleatoria para escoger de cual cadena se abstraerá el mismo, en caso que ξ sea menor o igual a OP se formará un doble enlace. De idéntica manera se hace con la subcadena y.
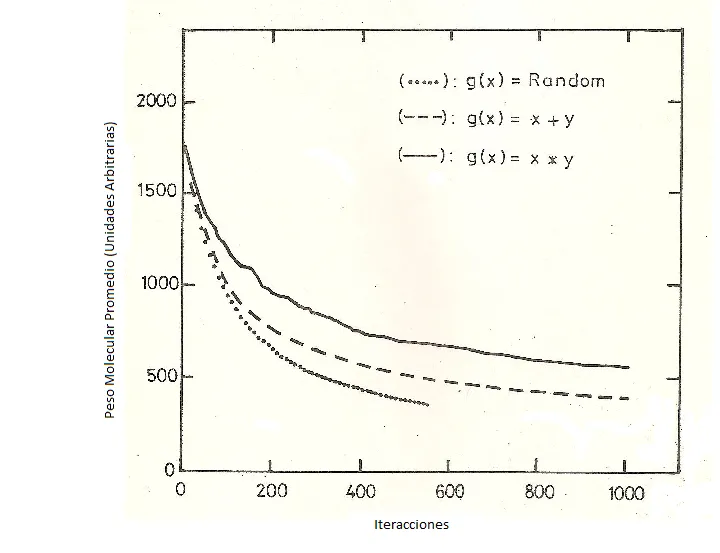
La ruptura de las cadenas poliméricas puede ser totalmente aleatoria o puede relacionarse con el tamaño de la cadena. Ziff (1) propuso una función de probabilidad g(x,y) que adquiere dos formas:
a) g(x,y) α x*y si la tendencia a romperse en el centro
b) g(x,y) α x+y si lo que importa es el tamaño de la cadena.
En la figura 2 se muestra un esquema del proceso para 10 cadenas de 10 unidades repetitivas. Como puede verse en la “matriz frontal” de colocan los operadores de ocupación correspondientes y en la “matriz posterior” el número correspondiente a la cadena. Cuando se produce una ruptura, las matrices son redefinidas: en la posterior, se mantiene la marca de la cadena de la subcadena x, pero la izquierda es remarcada. Por ejemplo: si hay 10 cadenas y se produce una ruptura, se colocará 11 como nueva marca. Si se produce entrecruzamiento, las cadenas que se entrecruzan cambian sus marcas convenientemente (la subcadena de mayor numeración toma el valor de la menor).

El algoritmo establece que los dobles enlaces son estables, es decir si se escogen un sitio ocupado por un operador 5 (=CH2) no se produce ningún cambio y se continua el proceso.
Es interesante notar, que en un proceso simplificado (donde solo se rompan las cadenas y no ocurran entrecruzamientos) hay una solución analítica para la ecuación diferencial sencilla que rige el proceso:
Donde Pmolecular es el peso molecular promedio y S la probabilidad de ruptura. La solución de la ecuación 1 es una exponencial decreciente.
En la figura 3 se muestra los resultados de la simulación al considerar los tres tipos de probabilidades: al azar (línea punteada), probabilidad (a) (línea interrumpida) y probabilidad (b) (línea continua).
Los resultados que se obtienen de la simulación son satisfactorios ya que al compararse con resultados experimentales realizados por el grupo de investigación con el que trabajaba daban un buen acuerdo, especialmente en los casos mostrados en las figuras 4 y 5 donde se hacía palpable que los procesos de entrecruzamiento no eran despreciables y que fueron publicados en la referencia 2 (de la que soy coautora).
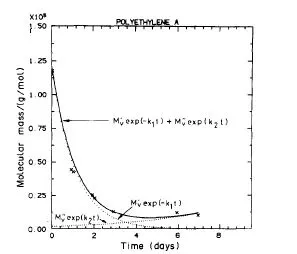
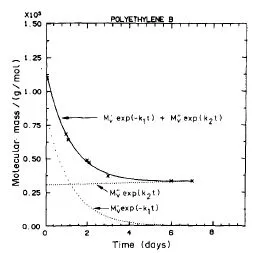
Las figuras que aparecen estan en las referencias 1 (en la que soy autora) y en la referencia 2 (en la que soy coautora).
Referencias:
- Chavez, E. Método MonteCarlo y sus aplicaciones. Trabajo de ascenso para optar a la categoría de agregado. LUZ. FEC. 1995
- Chirinos, A. y colaboradores. Eur. Polym. J. Vol. 23, No. 12, pp. 935 940, 1987.
- Ziff R. y McGrandy E. Macromolecules, 19, 2513, 1986.