Combinación de dos movimientos vibracionales perpendiculares

Combinación de dos movimientos vibracionales perpendiculares:

Las vibraciones u oscilaciones de los sistemas constituyen uno de los temas más estudiados de la física. Prácticamente todo sistema puede vibrar y existen muchas maneras diferentes de hacerlo. La característica de estos fenómenos es la periodicidad: las alas de un mosquito, la tierra durante un terremoto, el corazón de un ser vivo, entre otros.

Los movimientos armónicos son los muy variados y se dan en muchos sistemas que usamos cotidianamente como por ejemplo un resorte o el voltaje ac que alimenta nuestros equipos electrónicos.

En el caso de un resorte la fuerza que este ejerce sobre un cuerpo al que esté conectado cumple la ley de Hooke:

F=-Kx (1)
donde K es la constante del resorte y x la dirección donde se realiza el movimiento.

La primera ley de Newton expresa que F=ma donde m es la masa (considerada constante) y a es la aceleración del cuerpo.
Dado que la aceleración es a= d²x/dt² se nos plantea la siguiente ecuación diferencial 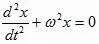cuya solución es para el caso unidimensional podría ser x=Acos(ωt) donde ω²=K/m (tambien podría ser una senoidal o combinación de ellas) .
Ahora abordaremos el estudio de dos vibraciones armónicas en direcciones perpendiculares ya que tiene un gran interés físico.
Consideremos que un punto sufre simultáneamente los siguientes desplazamientos(caso bidimensional):

x=A₁cos(ω₁t + α₁) (2)
y=A₂cos(ω₂t + α₂) (3)

Si seleccionamos adecuadamente t=0, podemos escribir el movimiento combinado como:

x=A₁cos(ωt ) (4)
y=A₂cos(ωt + δ) (5)
siendo δ la diferencia de las fases.
Analicemos algunos casos particulares:

δ = 0

x=A₁cos(ωt ) (6)
y=A₂cos(ωt ) (7)

por lo tanto,

y=(A₂/A₁)x (8)

El movimiento es una recta en dirección a la diagonal del rectángulo definido por las amplitudes tal que x e y tienen siempre el mismo signo (figura 1a).

δ = π/2

x=A₁cos(ωt ) (9)
y=A₂cos(ωt + δ) (10)

ahora se tiene que

x=A₁cos(ωt ) (11)
y=A₂cos(ωt + π/2)=-A₂sen(ωt) (12)
sabiendo que sen²(ωt )+cos²(ωt )=1, nos queda que:

x²/A₁²+y²/A₂²=1 (13)

Que es la ecuación de una elipse cuyos ejes principales coinciden con los ejes x y y. Esta trayectoria va en sentido de las agujas del reloj.

δ = π

En este caso también se tiene una línea recta como en (a) pero en la otra diagonal del rectángulo.

δ = 3π/2
En este caso resulta una elipse como en (b) pero el movimiento va en contra sentido de las agujas del reloj.

δ = π/4.

x=A₁cos(ωt) (14)
y=A₂cos(ωt +π/4 )= (A2/( sen(ωt)) (15)
En la figura 1 se muestra el movimiento resultante para δ= 0, π/4, π/2,3π/4,π,5π/4,3π/2, 7π/4, 2π. Esta figura se obtuvo con el siguiente programa fortran.

Figura 1
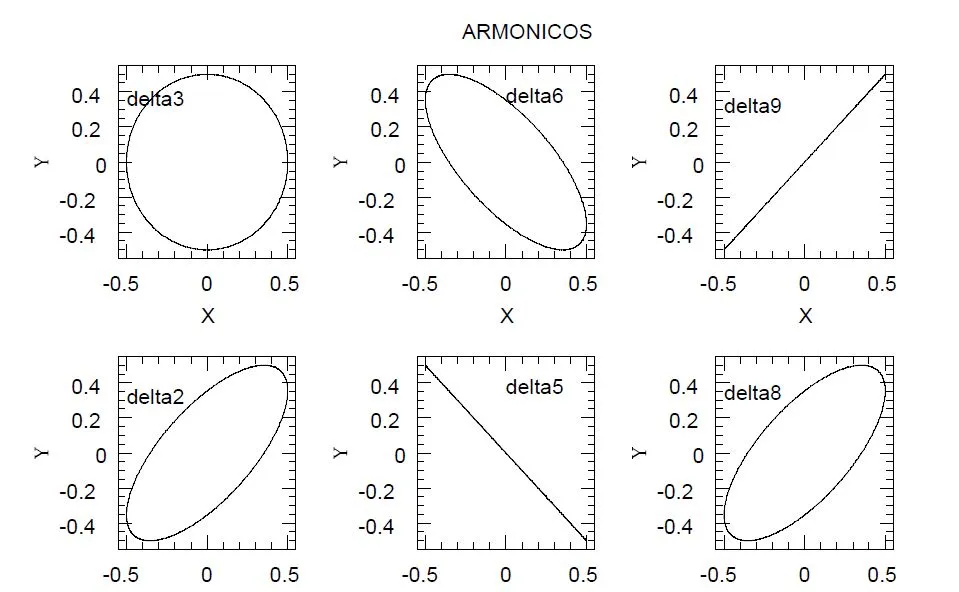
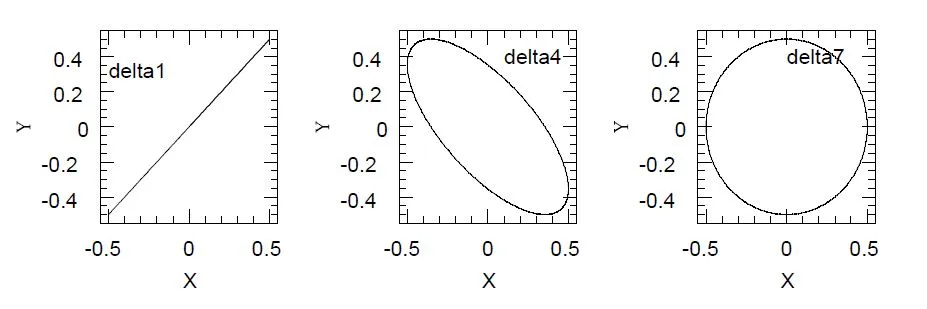
Patrones semejantes podemos encontrar en el caso de fuentes de voltaje ac. En la figura 2 (cortesía de @lorenzor) se muestra la salida de un osciloscopio con entrada de dos señales perpendiculares con una diferencia de fase de π/4.

Figura 2

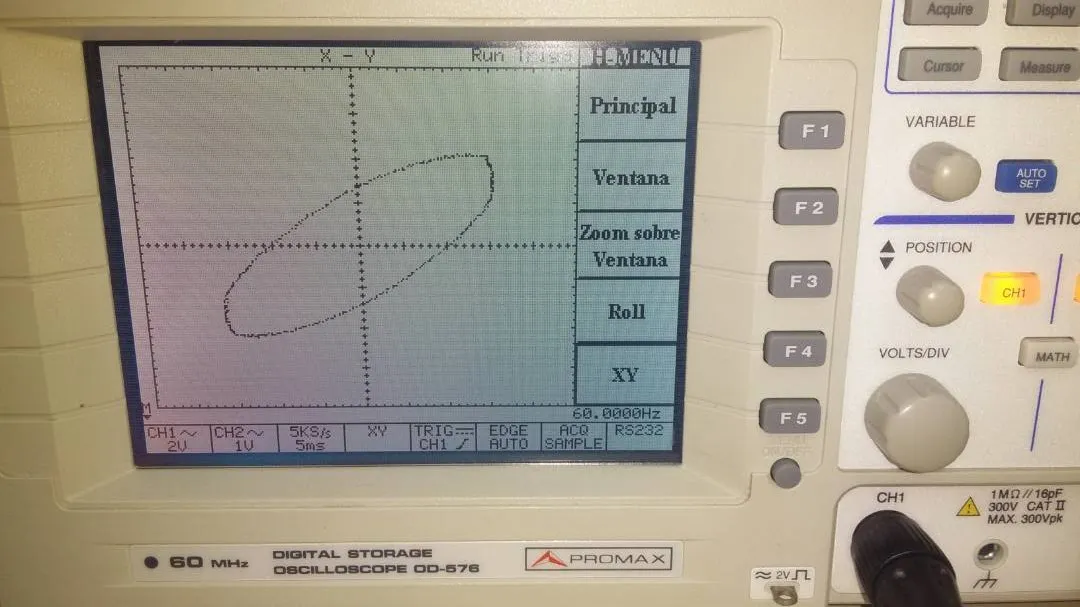
Un caso particular y que me ha llamado la atención y que deseo compartir con Uds. Es la medición de energía de los chacras. Para nadie es un secreto que en nuestro cuerpo se produce la transmisión de impulsos electromagnéticos. Obviamente, esto produce un campo que es mas o menos intenso dependiendo de la energía que metabolicemos.
Los chacras, en la cultura oriental son centros de energía. Hay 7 chacras principales y tienen una función que explicaré luego. Y una de las técnicas de medición es mediante un péndulo. Cuando hice el taller para medir la energía de los chacras se me recomendó el libro de Barbara Ann Brennan(2) (astrofísico que trabajo en la NASA) establece que la medición de la energía de esos chacras tiene patrones semejantes a los mostrados en la figura 1. Y Brennan en su libro asegura que se debe al campo morfogenético, al respecto establece:

En su libro A New Science of Life, Rupert Sheldrake afirma que todos los sistemas están regulados no sólo por los factores energéticos y materiales conocidos, sino también por campos invisibles de organización. Estos campos generan elementos causativos, toda vez que sirven de patrones para la forma y el comportamiento. Carecen de energía, en el sentido normal del término, porque su efecto va más allá de las barreras de tiempo y espacio que normalmente se aplican a la energía. Es decir, su efecto tiene una misma fuerza a larga y a corta distancia. Según esta hipótesis, cuando un miembro de una determinada especie aprende algún comportamiento nuevo se cambia el campo causativo de dicha especie, siquiera sea ligeramente. Si se repite el comportamiento durante el tiempo suficiente, su «resonancia mórfica» afecta a toda la especie. Sheldrake denominó a esta matriz invisible «campo morfogenético», de morphos, «forma», y genesis, «creación». La acción de este campo implica «acción a distancia», tanto en espacio como en tiempo. Más que una forma que es determinada por las leyes físicas al margen del tiempo, depende de la resonancia mórfica que atraviesa el tiempo. Quiere ello decir que los campos mórficos se pueden propagar a través, del espacio y el tiempo y que los acontecimientos pasados pueden influir sobre otros sucesos en cualquier otro lugar. Lyall Watson muestra un ejemplo de ello en su libro Lifetide: TheBiology ofConsciousness, en el que describe lo que ahora se conoce genéricamente como el principio del centésimo mono. Watson comprobó que, después de que un grupo de monos aprendiera un nuevo comportamiento, sus congéneres de otras islas próximas sin medios «normales» de comunicación también aprendieron repentinamente dicho comportamiento sin que en ningún momento se produjeran contactos directos. El doctor David Bohm afirma en la revista Revisionsque ese mismo efecto es aplicable a la física cuántica. Según Bohm, el experimento de Einstein-PodolskyRosen demostró la posibilidad de conexiones no locales, es decir, sutiles conexiones de partículas distantes. En consecuencia, la 22 integración del sistema sería tal que no se podría atribuir el campo formativo exclusivamente a una partícula, sino al total. Así algo que les suceda a partículas distantes puede afectar al campo formativo de otras. Bohm continúa afirmando que «la noción de las leyes intemporales que regulan el universo no parece sostenerse, porque el tiempo, en sí mismo, es parte de la necesidad que desarrolló». Rupert Sheldrake llega, en el mismo artículo, a la siguiente conclusión: «Por tanto, el proceso creativo que provoca el nuevo pensamiento, a través del cual se realizan nuevas entidades globales, es similar en ese sentido a la realidad creativa que da lugar a los nuevos entes totales en el proceso evolucionista. Se podría considerar que el proceso creativo es un desarrollo sucesivo de totalidades más complejas y de mayor nivel, a través de cosas previamente separadas que se conectan entre sí».

En mi experiencia, he medido chacras a muchas personas y la evaluación de los mismos ha coincidido con lo establecido por Brennan.
Le dejo un video donde hago una medición de chacras donde uso la técnica del péndulo (que explicaré en un próximo post)

Estas mediciones me han generado muchas preguntas y quizás este sea un espacio para interaccionar:
¿Por que se mueve el péndulo con patrones semejantes a los presentados en la figura?
¿Es posible calibrar estas mediciones?
También me ha llamado poderosamente la atención que la posición de los 7 chacras principales coinciden con las glándulas vitales como me muestra en la tabla 1

Tabla 1

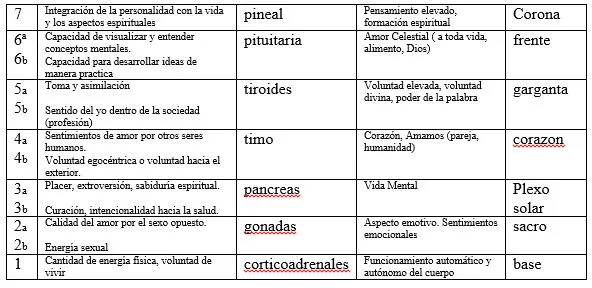
Nota : el 1 y el 2, corresponde a la parte frontal y posterior respectivamente.