
Hola amigos steemianos, esta vez vengo a compartir un problema que en su momento llegó a ser noticia en el New York Time´s, cuando una columnista de nombre Marilyn vos Savant (famosa por ser la mujer con más alto coeficiente intelectual ¡208!), según la revista de récord guines (El promedio de C.I para una persona común es de 100), brindó una solución a un peculiar problema propuesto por uno de sus lectores, para su columna “Ask Marilyn”, solución que resultó ser contra intuitiva y por esto levantó todo un revuelo intelectual y la crítica de un montón de matemáticos, y muchos profesores de Universidades prestigiosas en Estados Unidos. El problema de Monty Hall, inspirado por el concurso televisivo estadounidense Let's Make a Deal(Hagamos un trato), sin más preámbulos veamos de que se trata.

Artículo Monty Hall
Imaginemos por un momento que has avanzado hasta el final de concurso de TV, y vas por el premio final, un fabuloso auto 0 kilómetros, el presentador, te saluda y felicita y empieza el último concurso, te presenta 3 puertas frente a ti detrás de una de ellas tenemos el premio mayor un automóvil 0 kilometros, mientras que las otras dos tienen premios consuelo, cabras.
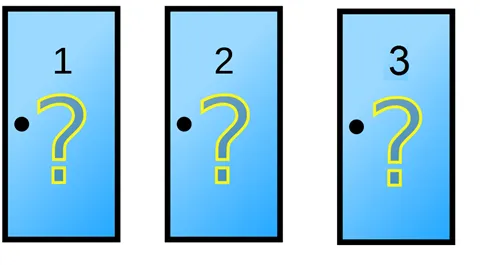
El presentador te dice que escojas la puerta de tu preferencia, (puerta 1, puerta 2, o puerta 3). Supongamos por decir algo que decides irte por la puerta número 1, él se posa frente a tu puerta elegida, te mira detenidamente, y procede a abrir una de las otras dos puertas, (EL SIEMPRE ABRIRÁ UNA QUE ÉL SABE QUE TENDRÁ UNA CABRA), en este caso por ejemplo procedió a abrir la puerta número 3 y pues vimos una cabra del otro lado, y aquí se pone interesante la cosa, se da la vuelta y te pregunta, si deseas cambiar la puerta que ya seleccionaste, por la puerta número dos?
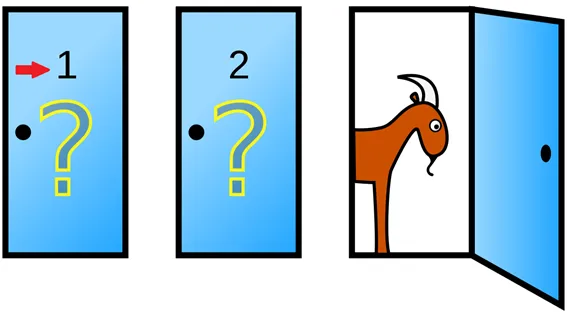
Es momento de tomar una decisión, ¿qué harías tu amigo lector cambiarias de puerta o te quedarías con la elegiste en primera instancia?

Si tu respuesta ha sido quedarte con la primera puerta seleccionada, porque decidiste que ese era tu número de la suerte, por superstición, o por una corazonada, déjame decirte que has tomado la decisión equivocada, al menos desde el punto de vista de la estadística, esta nos dice que conservando nuestra primera opción tenemos solo aproximadamente un 33% de haber acertado, y nos dice además que tenemos 77% de probabilidades de irnos a casa en una cabra.

Por otra parte, si tu decisión fue cambiar de puerta a la número dos, esta vez, has acertado, en hora buena, las posibilidades han estado de tu lado en tu decisión, con un % de éxito del 67% aproximadamente.

¿Cómo esto puede ser posible?, te aseguro que no es una broma, y procederé a demostrártelo de dos maneras. Primeramente por razonamiento simple, y el segundo si aún siguen sin creerme recreemos esto computacionalmente, y veremos quién tiene la razón.
Empecemos, por qué las probabilidades para cada opción son una en tres, 1/3, con la cual al escoger la primera vez, teníamos 1/3 de probabilidades de haber escogido el auto, mientras que teníamos el doble de probabilidades 1/3+ 1/3= 2/3, de haber escogido una cabra.

Sabiendo, que el presentador luego de que hagamos nuestra selección abrirá siempre una puerta que él sabe que tiene una cabra, lo sensato es cambiar de puerta, debido a que tenemos el doble de oportunidades de haber elegido una cabra a la primera, por lo que al cambiar a la única puerta que queda luego de que el presentador nos mostró la cabra es la del auto, aunque intuitivamente nos parezca que es lo mismo cambiar o no cambiar, al hacerlo las probabilidades nos estan diciendo que tendremos el doble de posibilidades de quedarnos con ese auto, y no de regresar a casa en una cabra, jejeje.
Si aún no me has creído déjame mostrarte los resultados de 20 millones de historias, o intentos de un pequeño código escrito en phyton que recreará nuestra situación en cuestión, y contará las veces que cambiamos de puerta y nos quedamos con el auto, y las veces que permanecimos fieles a nuestra primera decisión y nos fuimos a casa en una cabra.
Resultados de 10 millones de intentos. (Python corriendo en W7, 2GB de RAM procesador Celeron 1.46 GHz).
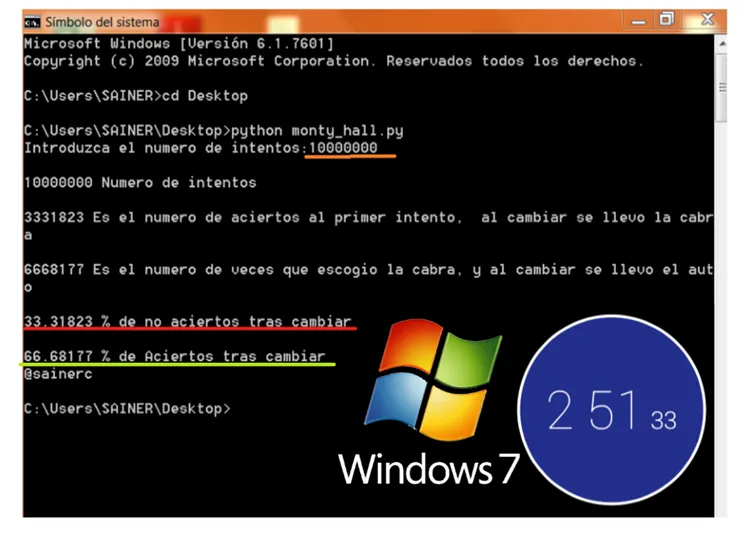
Resultados de 10 millones de intentos. (Python corriendo en Elementary-UBUNTU 16, 2GB de RAM procesador Celeron 1.46 GHz).
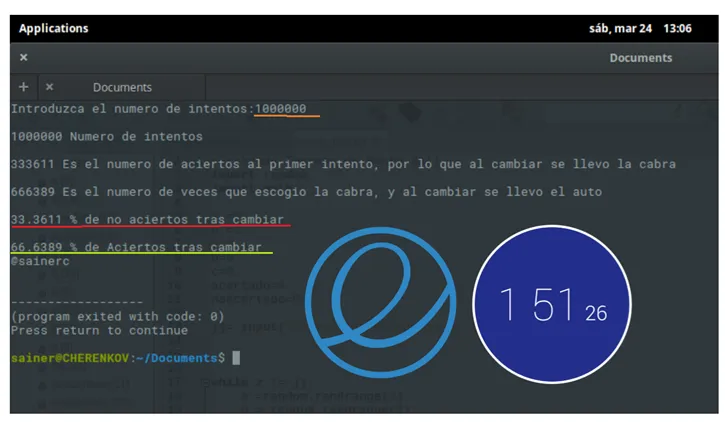
Como comentario aislado, vean que Linux corriendo exactamente el mismo código en idénticas circunstancias nos da resultado un porcentaje % más rápido que window equivalentes a tantos segundos.
Para quien le pueda interesar resumen del diagrama de Flujo del código.

Esto ha sido todo, espero que si se les presenta la oportunidad decidan cambiar de puerta sin dudarlo, Saludos queridos lectores.
REFERENCIA
Seyman, R. G. (1991), comentario sobre "Hagamos un trato: el dilema del jugador", A.m. Estadístico. 64 287-288.
Crockett, Zachary. (2015). El momento en que todos "corrigieron" a la mujer más inteligente del mundo. Priceonomics.