Hello Steemians, Merry Christmass to you all. I hope the Celebrations are full on with your family, friends and dear ones. Today I bring my new post on Quantum Computing as I promised. It is a revolutionary technology which will transform the face of our world and in future we may be Steeming in a much smarter way with the amazing technologies based on Quantum Computing. Lets see what Quantum Computing is.
Invention of Transistor in the 1947 gave birth to the revolution of Semiconductor Electronics which was imminent in the later decades. It grew manifold in the later decades ranging to various domains of life. As per Gordon Moore’s prediction the number of transistors per chip area grew double every eighteen month which added a multitude in the computing speed of the computers.
However, by the next few years this growth will reach its saturation as the size of the transistor will shrink to the size of an atom. At this dimension, Quantum Laws like Tunneling, Quantum Confinement etc. are prevalent and they hamper the normal operation of the transistors. It then prevents further minimization of the transistors and puts a saturation point on the computing power. Some organizations like the ITRS(International Technology Roadmap for Semiconductors)suggests some alternative devices(e.g. FiFET) which adds a minuscule computing power for few decades. However, these devices will also reach their saturation point in few decades.
There are certain problems in Computer Science, solving which requires a large computing power. For instance, the multiplication of two large prime numbers is an easy process. But, retrieving the two prime numbers from the product is almost impossible with our Classical Computers. The RSA Algorithm in Cryptography is based on this idea. No efficient Classical Algorithm has been designed till date which can solve the problem in a short time.
All these problems have a reliable solution in the form of Quantum Laws. The computer which uses the laws of Quantum Mechanics such as Entanglement and Superposition are known as Quantum Computer. For some applications Quantum Computers are exponentially faster than classical transistor based computers. Shor’s Algorithm, for example, is used to factorize a very large number in polynomial time. Similarly, Grover’s Algorithm can solve the binary search in a database in a very short time which a classical computer takes much longer time. Moreover, using Quantum Computers it is possible to simulate a Quantum System which is not possible in Classical Computers.
Quantum Bits or Qubits
The fundamental unit of Classical Information is bit which is denoted by the ON and OFF state of a MOS Transistor. When the transistor is in OFF state it denotes the logic state 0 and when in ON state it denotes the logic state 1. However, a transistor processes only one bit of information at a time. For larger information processing we need more than one transistors interconnected to form a large digital circuit. But, each of the transistors will have output as either ON or OFF state.
On the other hand, the fundamental unit of Quantum Information is Qubit(short for Quantum bit). A Qubit can be either in the state-0 or state-1 and a linear superposition of the states-0 and state-1. It means that they can be in both the states at the same time until we measure it. Because of this feature, in a Two Level Quantum System we can represent infinitely large amount of information unlike a classical bit.
Single Qubit
A Single Qubit can be represented with any two level quantum system e.g. the 1s and 2s state of the H-atom(Hydrogen atom) with one electron. This system can represent one Qubit of information if we denote the state of the electron being in the 1s energy state as the logic state 0 and the one being in the 2s energy state as the logic state 1.
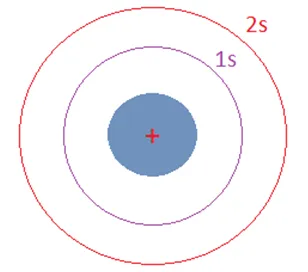
The logic states in quantum computation is denoted by using the "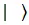
"notation as the states 
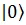and 
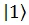. They can be in a superposition of the two states also which is denoted by,
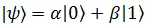
In the matrix form a Qubit is written as,
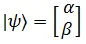
Hence, the states 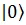and 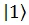can be written as, 
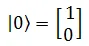and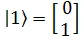 
.
Any measurement on the system disturbs the superposition and the system normalizes to one of the states i.e. 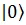or 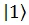with probabilities 
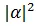and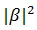 
respectively which satisfies the normalization condition,
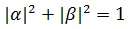
Multiple Qubit
A Multiple Qubit system can be represented by two or more two level atoms. An N-Qubit system can be represented with N H-atoms.
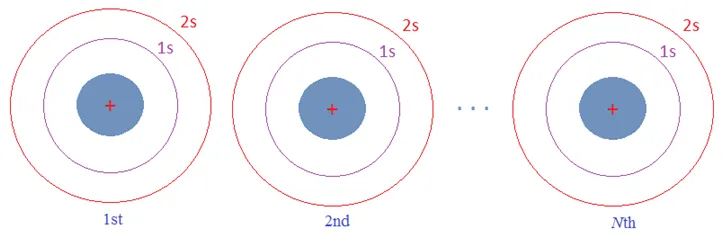
For example, a Two Qubit system can be represented with two H-atoms. The superposition state of a Two Qubit system is a 22=4 possible combination of all the states of the two atoms. It is denoted by,
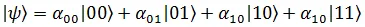
Which satisfies the normalization condition,
Quantum Computation: A Time Evolution Process
Quantum Computation is achieved in a quantum system which evolves with time. According to the postulates of Quantum Mechanics, Time Evolution of a quantum system is a unitary transformation and is described by the Schrodinger’s Equation,
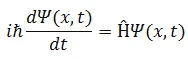
If a system is initially in the state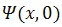 
, then at a later time 
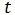, the state of the system is,
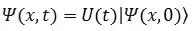
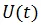is a unitary operator i.e. it satisfies the condition,
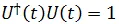
Quantum Gate
A Quantum Gate is a unitary transformation which can be described as,
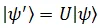
Where 
is a unitary operator i.e.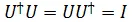 
Quantum Gates are of two types: Single Qubit Gates and Multiple Qubit Gates.
Single Qubit Gates:
A Single Qubit Gate operates on a Single Qubit. Some examples are as below:
Pauli-X Gate:
Pauli-X Gate is the quantum equivalent of the classical NOT Gate and is denoted by the symbol
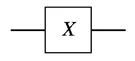
Pauli X-Gate is represented by the unitary matrix,
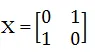
It operates on the state 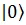to yield the state 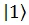as,
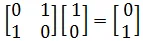
And on the state 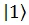to give the state 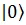as,
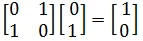
The X-Gate operation on the superposition state 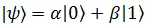yields the state, 
which in matrix form is represented as,
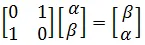
Square Root of NOT Gate:
A Square Root of NOT Gate is represented by the unitary matrix,
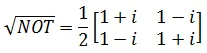
It is called the Square Root of NOT Gate because,
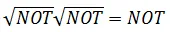
Hadamard Gate
A Hadamard Gate is denoted by the symbol,
And is represented by the unitary matrix,
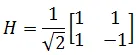
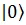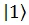A Hadamard Gate creates superposition state of equal probability by operating on the states and as,
Multiple Qubit Gates:
A Multiple Qubit Gate operates on a Multiple Qubit state. An example of Multiple Qubit Gate is:
CNOT Gate:
A CNOT Gate or Controlled NOT Gate is denoted by the symbol,
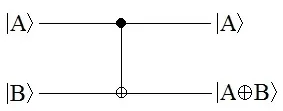
The top line is called the control qubit and the bottom line is called target qubit. The circuit works on a way that, if the control qubit is set to the state 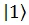, then the target qubit gets flipped, otherwise remains unchanged i.e.
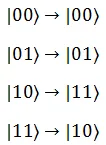
In matrix form CNOT Gate is represented as,
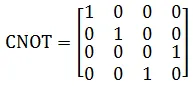
Quantum Circuits:
A Quantum Circuit is a combination of one or more Quantum Gates to implement a certain computational problem. Since, a Quantum Gate is a unitary operation, a Quantum Circuit also must be a unitary transformation. Now, the unitary nature of the quantum circuits implies that they are Reversible. It means that applying the inverse of the quantum circuit at the output of the gate we can recover back the original input states. This feature also a factor which makes Quantum Computers superior to Classical Computers.
Universal Quantum Gates:
NAND Gate is known as the Universal Gate in classical computation because, any classical circuit can be implemented by using only NAND Gates. A similar concept of universality exists in quantum computation. There are some sets of Quantum Gates using them any Quantum Circuit can be designed. Such sets of Quantum Gates are known as Universal Quantum Gates. The family of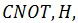 
the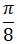 
gate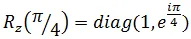 
gates is a set of Universal Quantum Gates. There exist other families of Universal Quantum Gates also.
Quantum Algorithms
Just like Classical Algorithms are implemented on Classical Circuits to perform classical computational problems, Quantum Algorithms are implemented on Quantum Circuits to perform quantum computational problems. Quantum Algorithms employ the concepts of Quantum Parallelism and Quantum Interference.
Quantum Parallelism is the property of performing more than one computation simultaneously. A classical processor processes only one computation at a time. To perform more than one calculation simultaneously classical computers need more than one processor interconnected, each processor performing one computation at a time. But, a Quantum Processor can perform more than one computation individually due to the superposition property of quantum states. This feature gives the Quantum Computers, a much larger raw computational power compared to a classical computer.
When two or more Qubit states are brought close to each other, they interfere with each other to form a superposition state much in a similar way two coherent light waves interfere.
Deutsch-Jozsa Algorithm: Superiority of Quantum Computers over Classical Computers
Deutch-Jozsa Algorithm named after its developers David Deutsch and Richard Jozsa in 1992 is a Quantum Algorithm which shows the superiority of Quantum Computers over Classical Computers in terms of computing power. The algorithm solves the following problem:
Suppose, Alice in Amsterdam selects a number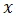 
from 0 to 2n-1 and mails it in a letter to Bob who is in Boston. Upon receiving the number 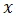Bob calculates a function 
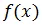and replies with a result 0 or 1. Now, 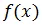is confirmed to be either constant or balanced. 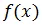being constant means that its value is either 0 or 1 for all 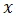. 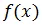being balanced means that for half of the values of 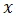, 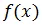is either 0 and for the rest half of the values of 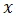, 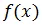is 1. Now, Alice’s job is to determine whether Bob had chosen constant or balanced, by corresponding to Bob as little as possible.
In a classical framework Alice needs to make at worst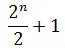 
queries to Bob to know whether 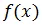is constant or balanced. It is because, Alice may get 
0s before finally getting 1, which proves that 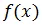was balanced. But, using Deutsch Jozsa Algorithm a Quantum Computer can prove with single evaluation that whther 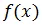is constant or balanced. Let us see how.
Instead of the classical calculation, the two decides to calculate 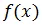using the unitary transformation 
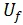. The whole circuit set up is shown in the figure below.
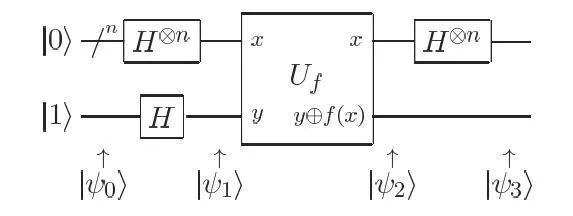
Alice has an n Qubit register to store her query and one Single Qubit register which she gives to Bob to store the answer in. Alice now prepares a state,
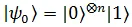
i.e. all the Qubits in the query register are in state 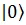and in the answer register the qubit is in 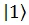state. She prepares superposition states by applying Hadamard Gates to the query registers as,
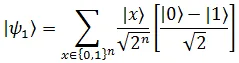
Now, Bob evaluates the function 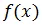by using 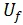as: 
which gives,
Alice, now applies Hadamard Transform to the query registers. Hadamard Transform on the state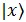 
can be written as,
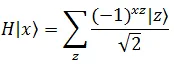
Hadamard Transform on an n-Qubit state is written as,
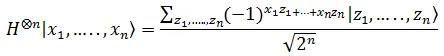
The equation can be written in a precise manner as,
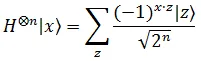
Now, the state after the Hadamard Transform can be written as,
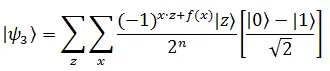
Alice now observes the query register. We notice that the amplitude for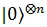 
is,
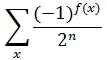
Now, if 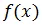is constant, then the amplitude of 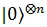is 1 or -1 and for all other Qubit states the amplitude vanishes because, the amplitude of 
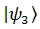is normalized to 1. If 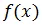is balanced, then the amplitude for 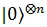vanishes as the positive and negative contributions to the amplitude cancel out to zero.
Hence, if Alice’s measurement results in all Qubits to be 0s, then Alice can say that 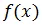is constant and if she gets at least one Qubit to be 1, then 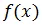is balanced. In this way Alice could decide with only one evaluation whether 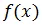is constant or balanced.
Many other Quantum Algorithms have been developed which proves the superiority of Quantum Computers over Classical Computers. Among them, Shor’s Algorithm and Grover’s Search Algorithm are the most popular ones. Shor’s Algorithm can factorize a very large number exponentially faster than a Classical Computer. Grover’s Algorithm is used to search an unsorted database in much smaller time than a Classical Algorithm.
Challenges of Quantum Computation
Building an efficient and reliable Quantum Computer is a challenging process. A Quantum System is very delicate to external environment. The electromagnetic noises in the environment causes disturbance and destroys the original state of the Qubits. For this reason, the system has to be isolated from the environment by keeping the system at extremely low temperature. It requires a lot of maintenance cost and the system becomes bulky. Researches are underway to to make Quantum Computers of the future much efficient and reliable.
Readers can watch the Documentary on Quantum Computing Posted by the Youtube Channel "PD Knowledge" below:
Though Quantum Computer is in its infancy we could easily foresee the revolutionary future it has, its impact on the world in the future. Quantum Computers will revolutionize the way how technology works. Quantum Computers will make early detection of Cancer possible, very efficiently by analyzing large number of factors causing the disease in a faster way. It will make weather forecast extremely efficient by analyzing a very large number of variables very quickly. Quantum Computers will be able to analyze vast numbers of data transmitted by the telescopes and help detect distant planets very easily. It will also help develop more effective drugs for superior drug based treatments. Quantum Computing is a major key to the success of Artificial Intelligence. From these facts it is well evident that the future of the world is much smarter compared to the present world. Quantum Computers will bring a revolution in much a similar way Classical Computers had brought in the last few decades. It is evident from the fact that most of the tech giants of the world like Google, IBM are in a rigorous race to develop Quantum Computers. Google is already developing driverless cars based on Quantum Computing. The race to develop these computing giants is bringing them close to a newer milestones every year to develop them for commercial purpose and well-being of human society. May be in a few decades we may start to see the impact of Quantum Computers in our life.
References:
- Book: Quantum Computation and Quantum Information by Michael A. Nielsen and Isaac L. Chuang
- Book: Quantum Chemistry by Ira N. Levine
- Youtube: Quantum Computing for Determined by Michael Nielsen
- Youtube Channel "intrigano": Quantum Mechanics and Quantum Computation by Umesh Vazirani
- Time: 9 Ways Quantum Computing Will Change Everything
- Quantiki: Quantum Gates
- Research at Google: Quantum A.I.
- Youtube Channel "Quantum Computing": Deutsch-Jozsa Algorithm
- Wikipedia
I hope you enjoyed learning about Quantum Computing. If you love dreaming and learning science then please follow me, @physics-o-mania
Don't Forget to Read My Previous Articles :
- Did the Science Channel Just Proved Ramayana to be Real!! Rama Setu or Adam's Bridge Not a Natural Creation, but Man-made
- Nikola Tesla: The Man of Electricity
- Quantum Cryptography and China's Quantum Satellite : A New Era of Hack-Proof Communication
- Einstein : The Person Who Made People Love Physics
- Mohenjo-Daro : A 4000 Years Old but Modern City
- Mining The Lunar Surface : A New Race in Space ?
- The ITER Project: Future of Endless Clean Energy?
- ISRO : The New Glamor in Space Race
- The Quest for the Grand Unification : The Theory of Everything
- The Hunt for the Dark Matter : The Unseen Neighbor
- The Strange Face of Reality : The Quantum Realm
If you are interested in various domains of Science and Mathematics then join the @steemstem project, team to support high quality STEM(Science,Technology, Engineering and Mathematics) related contents. Join them in steemit.chat to interact with the science authors from all over the world.
Thank you for reading my content !!
