
Hello steemianos friends, this time I come to share a problem that at the time became news in the New York Time, when a columnist named Marilyn vos Savant (famous for being the woman with the highest IQ 208!) , according to the Guines record magazine (The average CI for a common person is 100), provided a solution to a peculiar problem proposed by one of its readers, for its "Ask Marilyn" column, a solution that turned out to be counterintuitive and for this reason it raised a whole intellectual commotion and the criticism of a lot of mathematicians, and many professors of prestigious Universities in the United States. The problem of Monty Hall, inspired by the American television contest Let's Make a Deal, without further ado let's see what it is about.

Imagine for a moment that you have advanced to the end of the TV contest, and go for the final prize, a fabulous car 0 kilometers, the presenter, greets and congratulates you and starts the last contest, presents you 3 doors in front of you behind One of them we have the highest prize a car 0 km, while the other two have consolation prizes, goats.
The presenter tells you to choose the door of your choice, (door 1, door 2, or door 3). Suppose for saying something that you decide to go through door number 1, he perches in front of your chosen door, looks at you carefully, and proceeds to open one of the other two doors, (HE WILL ALWAYS OPEN ONE THAT HE KNOWS THAT HE WILL HAVE A GOAT) , in this case for example proceeded to open the door number 3 and then we saw a goat on the other side, and here it becomes interesting the thing, turns around and asks you, if you want to change the door you already selected, through the door number two?
It is time to make a decision, what would your friend reader change door or would you choose with the first choice?

If your answer has been to stay with the first door selected, because you decided that this was your lucky number, by superstition, or by a hunch, let me tell you that you have made the wrong decision, at least from the statistical point of view , this tells us that keeping our first option we have only about 33% of having hit, and also tells us that we have a 77% chance of going home in a goat.

On the other hand, if your decision was to change the door to number two, this time, you have hit, in good time, the possibilities have been on your side in your decision, with a success rate of approximately 67%.

How can this be possible? I assure you it is not a joke, and I will proceed to prove it to you in two ways. Firstly, by simple reasoning, and the second, if they still do not believe me, we recreate this computationally, and we will see who is right.
Let's start, why the probabilities for each option are one in three, 1/3, with which when choosing the first time, we had 1/3 of probabilities of having chosen the car, while we had twice as likely 1/3 + 1/3 = 2/3, of having chosen a goat.
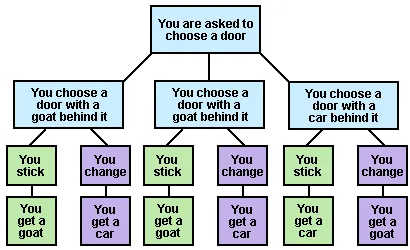
Knowing that the presenter after we make our selection will always open a door that he knows he has a goat, the sensible thing is to change the door, because we have twice the chances of having chosen a goat at first, so to change to the only door that remains after the presenter showed us the goat is the car, although intuitively we think it is the same to change or not change, in doing so the odds are telling us that we will have twice the chances of staying with that car, and not to go home in a goat, hehehe.
If you still have not believed me let me show you the results of 20 million stories, or attempts of a small code written in phyton that will recreate our situation in question, and count the times we change the door and stay with the car, and sometimes We remained faithful to our first decision and went home in a goat.
Results of 10 million attempts. (Python running on W7, 2GB of Celeron processor 1.46 GHz RAM).
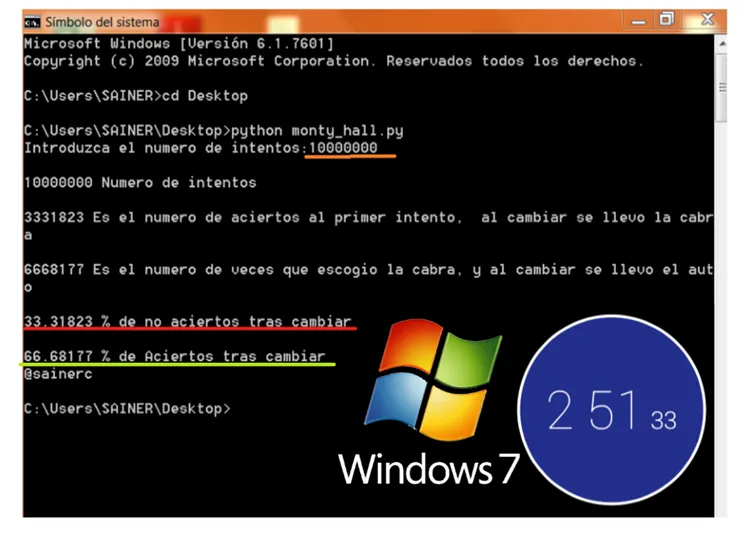
Results of 10 million attempts. (Python running on Elementary-UBUNTU 16, 2GB of Celeron processor 1.46 GHz RAM).
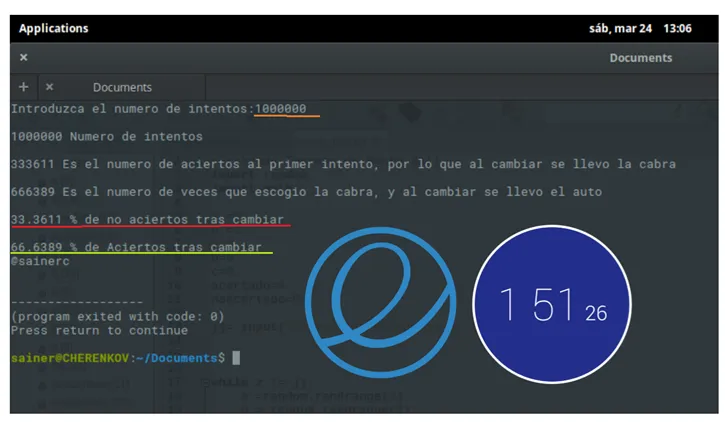
As an isolated comment, see that Linux running exactly the same code in identical circumstances gives us a percentage% faster than window equivalent to so many seconds.
This has been everything, I hope that if the opportunity presents itself they decide to change the door without hesitation, Greetings dear readers.
REFERENCE
Seyman, R. G. (1991), comment on "Let's make a deal: the player's dilemma", A.m. Statistical. 64 287-288.
Crockett, Zachary. (2015). The moment when everyone "corrected" the most intelligent woman in the world. Priceonomics.