In 2000, Clay Mathematics Institute selected seven unsolved problems in mathematics and put Million dollar prize for solving each problem. These seven problems are known as the Millennium Prize Problems. As of today, only the Poincare conjecture has been solved ( solved by Grigori Perelman in 2003). In this article, I want to talk about my favourite one: "The P vs. NP Problem"[1].

P Problems
Let's begin with a simple mathematical addition : 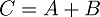
If I give you the value A=2 & B= 3, you can instantly calculate the value of C, which is 5
What if I give you the value A=5,B=2 and C=6 and ask you to check the whether the given value satisfies the equation? Again this is as simple as calculating the value of C in the previous step. We can derive a simple conclusion from this:
- The addition problem is easy to solve
- The addition problem is easy to check
We categorise this class of problem as "P" problems. ( polynomial time)
NP Problems
Now think about sudoku. Suppose I give you an unsolved Sudoku, you can't come up with a solution instantly but if I give you a solved Sudoku then you can easily check the validity of the solution.
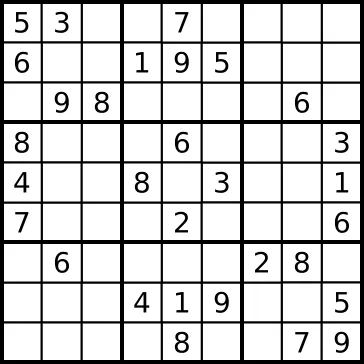
This leads to following conclusions:
- Sodoku is difficult to solve but
- Easy to check
Now we have a different class of problem: "NP" problems (Non-deterministic polynomial time).Another simple example of NP problem is a jigsaw puzzle. Jigsaw puzzles are difficult to solve since there are thousands of possible combinations but checking the validity of a jigsaw puzzle is easy, even children can do that.
We have two sets of problems "P" and "NP" , and every mathematical(or computational) problem can be categoried into the two sets. Its either "P" or "NP" , and finally the P vs NP problem:
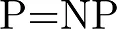 or
or 
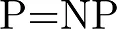 or
or 
The question is: Whether all NP problems are just P problems (P=NP) or fundamentally the NP problems are different from the P problems(N does not equal to P) ?
We have stated the fact that Sudoku problems are NP problems but can we come up a better Sudoku solving algorithm and render sudoku as a P problem? we know that every P problem is an NP problem, i.e. P is a subset of NP. What we want to know is if the reverse is also true?
We have been classifying problems as "easy" and "difficult" but these words don't mean anything to a computer. To compare the time consumed by an algorithm we have to use the Big O concept.
Big-O[2]
Now you may argue that though Sudoku problems are difficult for us humans, a computer can solve them pretty fast. Yes, even our smartphones can solve 9x9 Sudokus in less than a second but what happens when the scale of the problem goes up? Can our computers catch up with the problem scaling? Give a 1000x1000 soduku to a computer and the time taken by the computer will grow exponentially but this doesn't happen for P problems, even large multiplication problems are easily solvable by computers.We are concerned is with how the runtime of an algorithm increases with its input? Back to Big O.
Big O is a concept in computer science to quantify the performance of algorithms. Let us compare two ways of transferring data:
- A pigeon carrying a 1 TB flash drive
- Downloading data from the internet.
Up to 1 TB, the time taken by the pigeon to transfer the data from one place to another doesn't depend on the size of the data, the pigeon would take the same time to transfer 1 KB or 200 MB. We call this the Big O of 1, O(1)
An example of O(1): Checking whether a number is even. No matter how big the input is, the time taken by the algorithm is constant.
But in the case of downloading data from the internet, the time required to download 1 MB and 200 MB isn't the same. This is the case of O(n), where n is the size of the data.This means that the time taken to download the data depends linearly on the size of the input.
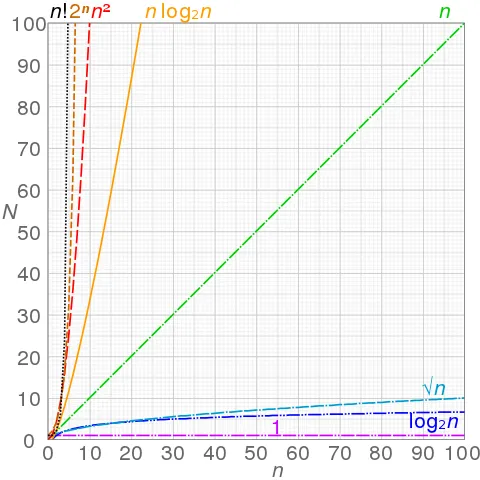
There are Big Os with higher power too; O(n2), O(n3) and even exponentials exist; O(2N). The graph below shows some of the typical Big Os. On the X-axis we have the input variable as n(size of the input) and on the Y-axis we have the output variable as N(time required for computation).
Let's look at the two most impotant ones:
- Polynomial: O(nK), K = 0,1,2,3,.. <<<<<<<<<< Good Algorithms
- Exponential: O(2n), O(100n),... <<<<<<<<<<<< Bad Algorithms
As you can see, the polynomial(n and n2) increases slowly in comparision with the exponential. We always want to avoid the exponential and factorials for problem solving algorithm but sadly the NP problem algorithms fall into this "bad category".
Back to P vs. NP
Hope you got the underlining principle of Big O. This will help us understand P and NP problems in detail ;)
Checking the solution of a Sudoku is in Polynomial time ( O(NK), but do we have an algorithm for solving sudoku that operates in poly time too( just like checking it)? So far we don't have any algorithms for that. This leads us to categorize the Sudoku in NP class.
The time required to solve sudoku increases exponentially as its size increases but the time required to check the solution of solved sudoku increases linearly
In the case of P problems, both the checking and solving fall into the Polynomial-time category. Hence they are easier to solve and check, even if the input size is large. If we can find algorithms for NP problems that operate in Polynomial time too, then the P vs. NP problem will be solved but sadly we don't have those algorithms.
There are more!
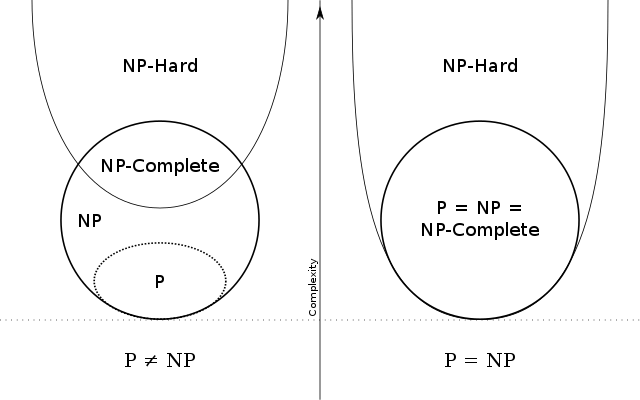
The subclasses of problems aren't just limited to P and NP, there are more. We have only touched the tip of the iceberg. We have something even harder than NP: The NP-hard problem, they are at least as hard as NP problems but not all NP-hard are NP, so the intersection of NP-hard and NP is the NP-complete. There is another interesting one, which category is best suited for chess? Solving chess is difficult and checking a solution isn't easy either, it doesn't satisfy the criteria for either P or NP, and this results in another class of problem; "EXPTIME-hard". I can go all night on this but let's focus only on P and NP.
Does it even matter?
Let's suppose that I proved P=NP and won the Million dollar. The implication of this would be enormous. The internet would take the first blow. The whole of internet relies on public key cryptography (prime factorization) but now theoretically we could crack the entire security system. The entire cryptocurrency market is based on the assumption that P!=NP. Basically crypto would die. There is a problem though, even if we manage to prove that P=NP, we still have to develop constructive algorithms for NP problems. Just proving P=NP won't do much. Polynomial algorithms are faster than exponentials but it doesn't necessarily mean that polynomial time will be a reasonable time. Even if someone proves P=NP by developing a poly-time algorithm with O(N100), our public key cryptography would still be safe.
On the other hand, the positive impact would be enormous too. The implications would be big in mathematics. If you manage to prove P=NP, then you might take home Six million dollars instead of one, since solving the other 5 millennium problems would be a lot easier. Another benefit would be in the field of optimization. Multivariable optimization problems pop up in most fields of science, we rely on giant supercomputers and slow algorithms, but with P being equal to NP, these optimization problems could be solved as easily as they can be verified. Protein-Folding is also an important NP-Complete problem. Just like an object falls under the action of gravity to reduce its potential energy, protein molecules fold themselves to minimize their chemical energy, and it turns out that the behaviour of a protein molecule depends on its geometrical shape. Prediction of protein structure correctly would open new frontiers in drugs development.
The implications of the theorem being right, either way, are too much but don't get your hopes too high on P=NP. Most of the computer scientist and mathematicians don't believe P to be equal to NP. In fact, a poll created in the University of Maryland back in 2002 revealed that 69 % believed P!=NP, 9 % supported the opposite and the rest weren't sure about the answer.
Finally, I want to quote Scott Anderson, a complexity researcher at MIT:
If P = NP, Everyone who could appreciate a symphony would be Mozart; everyone who could follow a step-by-step argument would be Gauss; everyone who could recognize a good investment strategy would be Warren Buffett.
My opinion: I am a firm supporter of P!=NP, I know opinions don't matter in mathematics, and this problem might remain unsolved for decades or centuries but until then we have to assume P!=NP. Cheers!
References:
1. http://www.claymath.org/millennium-problems/p-vs-np-problem
2. https://brilliant.org/wiki/big-o-notation/
3. https://math.berkeley.edu/~kpmann/encryption.pdf
4. Guyeux, C., Côté, N. M., Bahi, J. M., & Bienia, W. (2014). Is Protein Folding Problem Really A Np-Complete One? First Investigations. Journal of Bioinformatics and Computational Biology, 12(01), 1350017. doi:10.1142/s0219720013500170
https://arxiv.org/abs/1306.1372
5. https://www.newscientist.com/article/dn21578-poll-consensus-on-million-dollar-logic-proble
6. https://brilliant.org/wiki/p-versus-np/
7. https://cacm.acm.org/magazines/2009/9/38904-the-status-of-the-p-versus-np-problem/fulltext


If you are new on steemSTEM or just want to be a part of the community, the please join us on our Discord channel and please check out the posts on #steemstem!