Take a look at this map of United States. You can see the 50 states shaded by different colours. Not just different but four colours to be precise. Also, notice that no two adjoining states have the same colour. You may be like duh! What’s so special about all this? Just give me few more seconds.
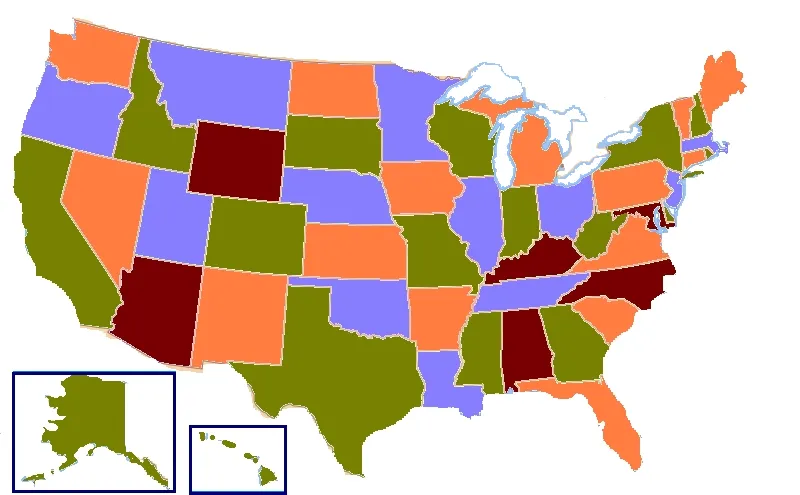
What if I told you that any map, real or hypothetical, can be coloured by using just 4 colours!! YES, ONLY FOUR.
Is it just because the United States isn't that big? Take a look at the world map below. YES, only four colours are needed to colour the whole earth.
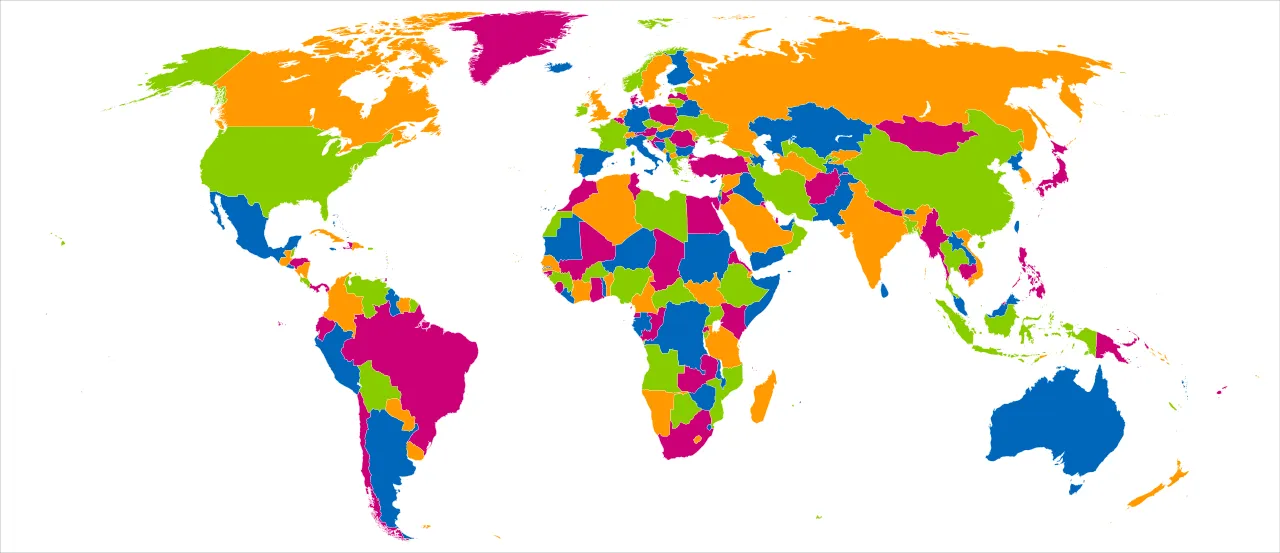
You think it is a mere coincidence? I will show you a few more. And yes, this works for hypothetical maps too!

Here's a map of giant Russia that uses 4 colours only.
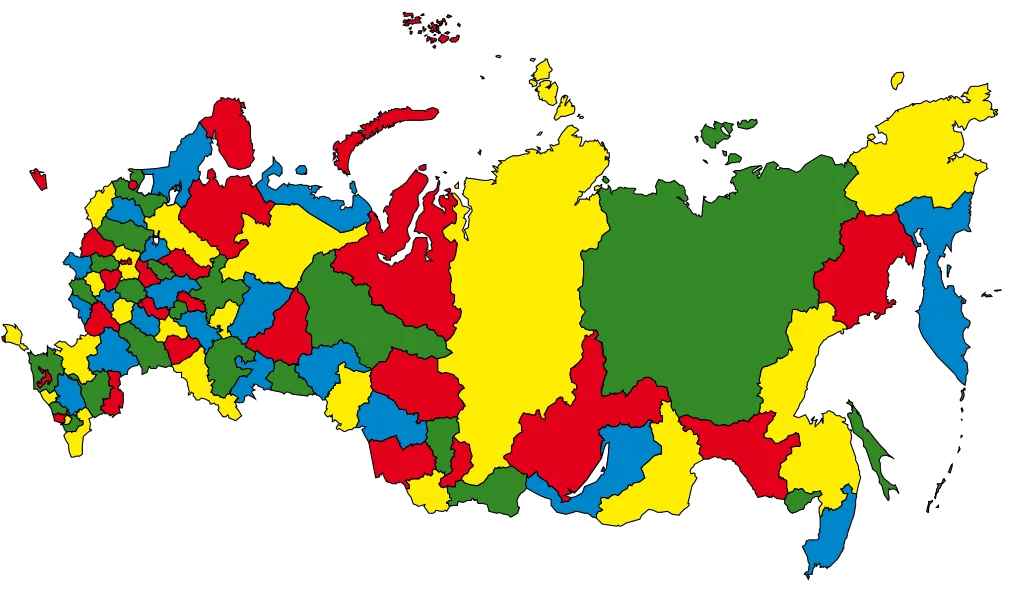
This is the famous four colour map theorem
Now at this point, your brain might be in a panic mode. Seriously how is it even possible?
At first, it is pretty difficult to wrap your head around this theorem. Every part of human mind tries to deny the fact that only four colours are needed no matter how big or complex the map maybe. But the good thing is that this is a proved theorem, so no need to spend your effort on designing a new map. ; )
I think it will be insightful to know how this theorem even came into being.
History
First of all, this wasn't discovered as a problem of mathematics. Instead, a guy named Francis Guthrie discovered that only 4 colours were needed while he was trying to colour the map of counties of England in 1852. But Francis’s brother, Frederick, was a student of the famous mathematician Augustus De Morgan. The problem was presented to De Morgan but the theorem remained unproved after several failed attempts.
Even after the death of De Morgan, several attempts were made by various mathematicians. One widely acclaimed proof, which later turned out to be wrong, was given by Alfred Kempe in 1879. Although Kempe's proof was flawed, it later gave rise to Five Colour Map theorem. This is same as the four colour map theorem except that it requires five colours. The great thing is that the Five colour map theorem is a lot easier to prove and later this laid a foundation for the proof of Four colour map theorem.
Finally, the theorem was proved in 1976 by Kenneth Appel and Wolfgang Haken. It took 125 years and generations of mathematicians. The proof surely made headlines during the 70s but it also remained controversial, since it was the first major theorem that was proved using a computer.
YES, the first.
A formal statement of the theorem:
Any planar map can be coloured using four colours such that no two neighbouring regions are of same colour.
Proof
First, the proof isn't easy. Remember, it took 125 years to prove it! Also, the full proof of this theorem isn't possible here. I will just give you the general idea around which the proof is based. I will try my best to keep it simple as possible. The first thing we do is to make use of "networks" to reduce any map. Let's consider a very simple map.
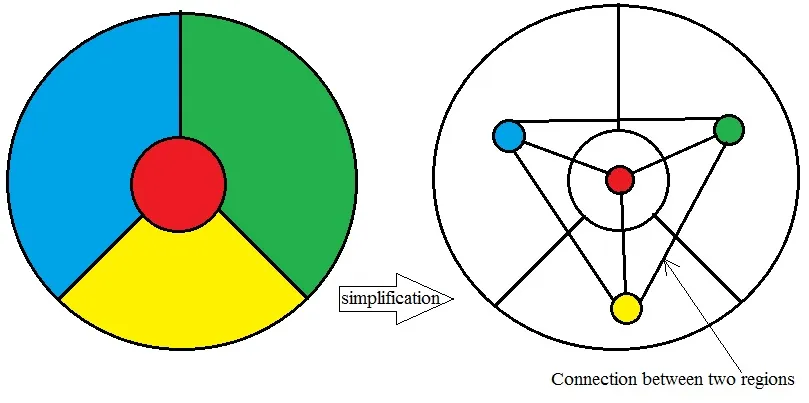
source: made by myself
On the left side of the image, there is a map with four regions. Four colours are used to colour the map. Now what we have done on the right side is that the coloured regions are represented by small coloured balls and the borders of the regions are shown by the connecting lines. The resulting diagram is the network diagram of the map. I will show you another example.
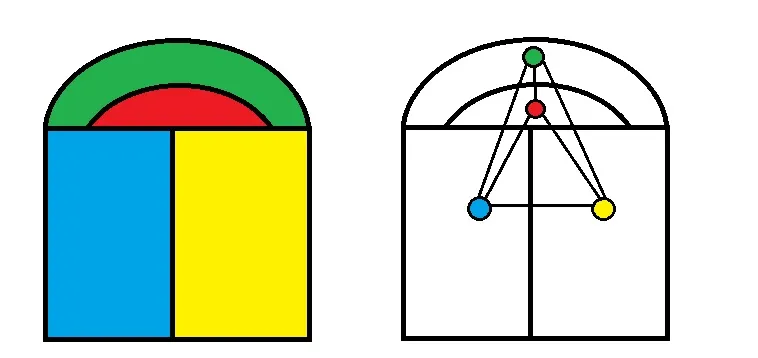
source: made by myself
This second map looks more complicated than the first one but if you look at the network diagram on the right, both maps have the same network diagram. This means that though the maps look different to us, mathematically they are virtually the same thing! The benefit of using network diagram is that we can reduce very complex looking maps into a simpler form and also the numbers of maps can be reduced because many maps that may look different are actually the same.
To prove or disprove the theorem (or conjecture, when it wasn't proved) we have two options:
- Show that every map needs four colour. OR
- Show at least a single map that needs five colour.
No one has been able to come up with a map that needs five colours but just because we don't have any map that requires five colours doesn't mean that the conjecture is proved. So what we have to do is prove that every possible map can be coloured with four colours. But you may think that there are infinite numbers of possible maps and how is it possible to prove the theorem for an infinite number of maps? Yes, indeed there are infinite numbers of possible maps but if we use the network diagram concept, it can be shown that there are large but finite numbers of planar graph. This is the basis behind the Appel–Haken proof.
Appel-Haken proof
The proof they did is a bit tricky. At first they created a list of networks in a such a way that every possible map must contain one of these networks. The made a list of 1936 networks! Then they proved that each of the networks they listed can be coloured using just four colours. The difficult part of this proof was that it was hard to prove that every one of the networks can be coloured using four colour. Now comes the controversial part. They used a computer to prove the four colour theorem for each one of the 1936 networks. It would be nigh impossible for us humans to do by hand. The reason behind the controversy was maybe the fact that it was the first computer-assisted proof in mathematics.
Here's a page from the Appel-Haken paper, published in 1977, that shows some of the possible networks:

Exception
How can there be an exception to a proved theorem? The exception is not in the part of the theorem but rather in the use of the theorem for real maps. The requirement for the theorem to be true is that the regions must be contiguous, i.e. all the regions must touch each other. Unfortunately, this doesn't always hold true for real maps. Just look at the map of the United States. The state of Alaska is not contiguous with the rest of United States. Instead, there is an ocean that requires a separate colour. So the colouring the world map ( including ocean) using just four colour would not be possible.
References
- History
- Proof
- Proof: Appel, K.; Haken, W. Every planar map is four colorable. Part I: Discharging. Illinois J. Math. 21 (1977), no. 3, 429--490.
steemSTEM
