One of the major law of nature is the second law of thermodynamics. Actually, there are altogether four laws of thermodynamics but the second law is the most interesting one. This article is about a thought experiment which seems to violate the second law of thermodynamics! Yes, you heard me right. This sounds like something a flat-earther would say but this thought experiment was devised by none other than the famous physicist, James Clerk Maxwell.

First, Let's get familiar with the second law of thermodynamics.
The total entropy can never decrease over time for an isolated system.
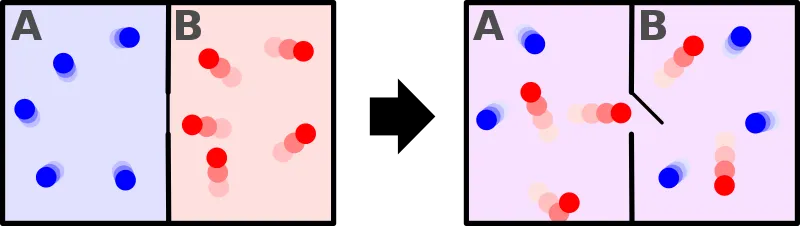
There are many ways of stating the second law but I will stick to this one. The statement above means that heat energy will never flow spontaneously from a cold object to a hotter one. Take a look at the picture below, there are two compartments each with air at a different temperature. The compartments are separated from each other by a thermally insulated wall with a small door, which is closed for now. let's say the blue one is at 10 °C and the red is at 50 °C. What happens when we open the door connecting the compartments? General intuition tells us that the air at 50 °C loses its heat energy to the other one until the system acquires a thermal equilibrium. This "General Intuition" is, in fact, the second law of thermodynamics. The second law is all about the direction of the flow of heat energy. From entropic point of view, the system changes from an ordered state to a disorder one. Up to now, we haven't violated any laws but will the disordered state go back to the ordered on its own? The second law tells us that it won't but Maxwell's demon tries to defy the second law. Yes, in the thought experiment devised by Maxwell, the entropy increases! Before we dive into the thought experiment, we need to understand a bit about the concept of temperature.
Temperature
We relate temperature with hotness and coldness but from a scientific perspective, the words don't have any meaning. A summer day at 40 °C feels hot for us but in comparison with the temperature of the sun, our summer day is too cold. To avoid this relative conundrum, we use a scientific definition of temperature. Quantitatively, we define temperature as:
The measure of the average kinetic energy of molecules.
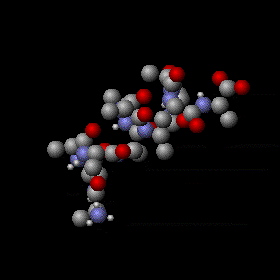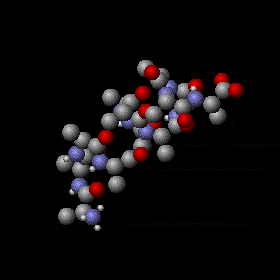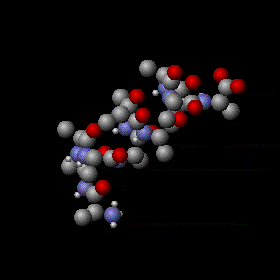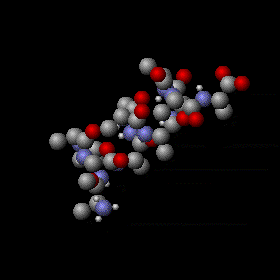
Molecular vibration of a segment of protein alpha helix by Greg L,CC BY-SA 3.0
Kinetic energy is the measure of the vibration and movement of the molecules of a system. In the case of a solid object, the molecules are constantly vibrating and higher the temperature, higher is the amplitude of vibration. Similarly, for a gas, the temperature is the measure of movement of the molecules. This is described by the kinetic theory of gases. The universal scale of temperature measurement, which is the Kelvin scale, is based on this definition of temperature. As the temperature decreases the vibration/movement of molecules decrease and eventually we reach a state when the vibration completely ceases. This temperature is the zero Kelvin.
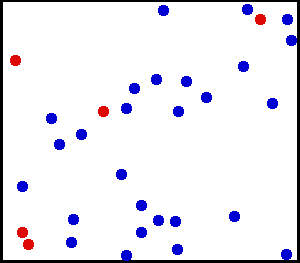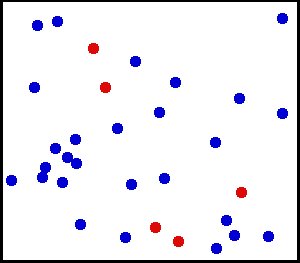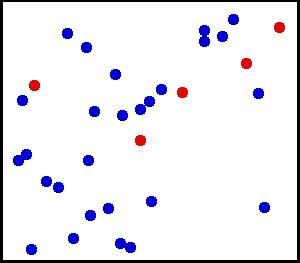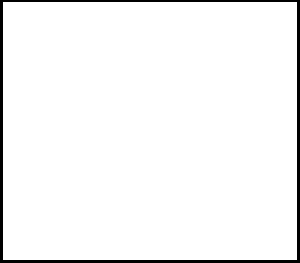
Motion of gas molecules by Greg L, CC BY-SA 3.0
If you look closely at the definition of temperature, we have used the term average kinetic energy of molecules. This plays a crucial role in our thought experiment, pay more attention to this :) Let's say we have air at 25 °C. Since the temperature is above zero kelvin, there will be movement of molecules and the molecules have a certain amount of kinetic energy but do all molecules have the same kinetic energy, i.e. do all molecules move with the same velocity? The answer is no, they don't. Look at this gif picture of gas molecules constantly moving and colliding with each other. The movement and collision are random processes and the molecules have different velocity at each instant. There are countless numbers of molecules, so how can we know the velocity of each molecule? For this, we use the Maxwell–Boltzmann distribution
Maxwell–Boltzmann distribution
We have established the fact that gas molecules don't move with the same speed and now we want to know the speed of those molecules. Is it possible though? There may be millions of molecules and we don't have any deterministic way to find the velocity of each molecule. To solve this, Maxwell and Boltzmann ( independently) formulated a statistical method. I won't go behind the mathematics of Maxwell-Boltzmann distribution but a graph of the distribution will be enough to understand the general principle.
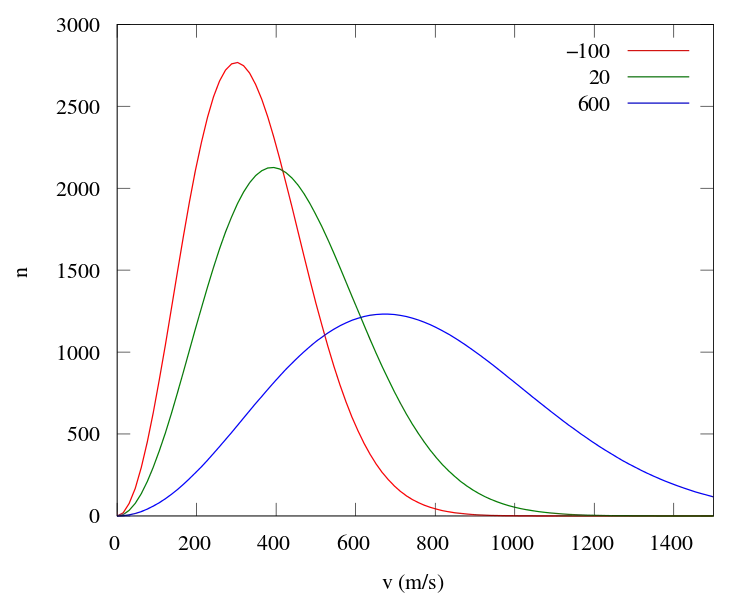
The horizontal axis shows the speed of Oxygen molecules, the vertical axis shows the number of Oxygen molecules and the three different coloured plots are for three different average temperature.
Red: -100 °C
Green: 20 °C
Blue: 600 °C
This is actually a probability distribution and it gives us a probability of finding molecules at a specific temperature range. Let's look at the red one. The average temperature of the red is -100 ° C. At this temperature the average speed of the molecules is 338 m/s but we know that all molecules won't move at this speed. Since the peak is at 300m/s, we will find most molecules moving at this speed but there are also those molecules which are moving much slower or faster than the average speed. For example, there are around 100 molecules moving at 800 m/s, which is much faster than the average speed. There are also slow-moving molecules. The fact that not all molecules move with the average speed is the key concept used in Maxwell's thought experiment.
Maxwell's Demon
In his book Theory of heat (1872), Maxwell wrote about a being that could violate the second law of thermodynamics:
... if we conceive of a being whose faculties are so sharpened that he can follow every molecule in its course, such a being, whose attributes are as essentially finite as our own, would be able to do what is impossible to us. For we have seen that molecules in a vessel full of air at uniform temperature are moving with velocities by no means uniform, though the mean velocity of any great number of them, arbitrarily selected, is almost exactly uniform. Now let us suppose that such a vessel is divided into two portions, A and B, by a division in which there is a small hole, and that a being, who can see the individual molecules, opens and closes this hole, so as to allow only the swifter molecules to pass from A to B, and only the slower molecules to pass from B to A. He will thus, without expenditure of work, raise the temperature of B and lower that of A, in contradiction to the second law of thermodynamics.
Theory of heat, p. 338 [1]
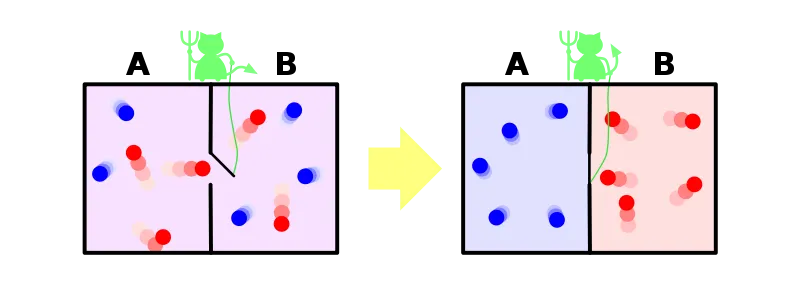
This being was later dubbed as "demon" by Lord Kelvin because it would cause serious havoc by breaching one of the fundamental laws of nature [2]. Look at the picture below. There are two compartments each with air at the same temperature, let's say 50°C. There is a molecular-sized mass less door connecting the two compartments and the demon is in control of the door. This so-called demon isn't something you would see in movies or paintings. The demon is actually an entity that has the ability to know the temperature of each molecule. Think it as a nano-scale sensor. We have already established the fact that there are molecules which move much slower or faster than the average speed. Now comes the role of the demon. Since the demon has the ability to know the temperature of each molecule, it will open the door in a such a way that fast molecules(reds) will travel to the right compartment and slower molecules (blue) will travel to the left compartment. In the end, we have a system of two compartments with air at an unequal temperature and the demon did this without using any external source of energy. The second law doesn't allow this. Think about the refrigerator, it transfers heat from a hot region to a cold region but it uses electric power to do this. On the other hand, the demon did the same thing without using any source of energy. Voila! We violated the second law of thermodynamics. This means free energy! we can finally have perpetual machines, no more environment unfriendly fossil fuels. Sadly no, we won't have any perpetual machines. We can't let a demon defy our precious second law, and finally the exorcism.
Exorcism
I would love to see a perpetual machine but mother nature won't let that happen. The second law has to be true, so where did the thought experiment fail? Before going into exorcism we should know that Maxwell never intended it to breach the second law practically. He wanted to convey an idea that through molecular manipulation one could fail the second law. Without further ado, let the exorcism begin! The first argument that comes to mind in the existence of the demon. Can a molecular level demon capable of measuring the temperature of each molecule even exist? Practically such thing doesn't exist but we are more concerned with the measurement of temperature with such precision rather than the size of the demon. During our whole analysis, we haven't talked about the work done by the demon to measure the temperature. No matter how the demon measures the temperature, energy has to be used. The measurement of temperature increases the entropy by more amount than the demon could decrease the entropy by switching the molecules. Physicists were confident that measurement process would generate entropy and they assumed the demon to be dead.
The demon was revived when Leo Szilard (in 1929) developed a hypothetical engine in which a demon appears to lower the entropy of a heat engine with a single molecule as working fluid [3] I will briefly explain about the Szilard's engine.
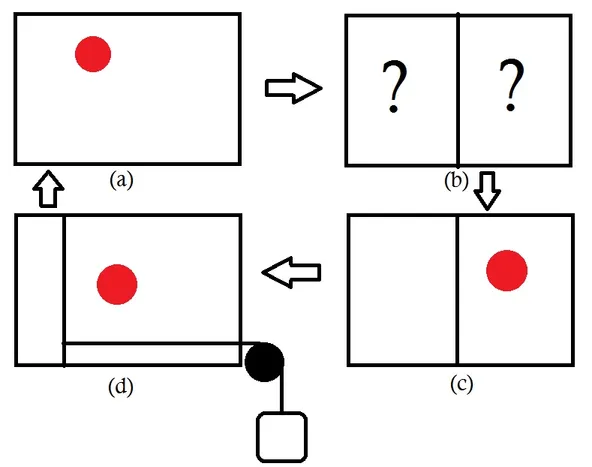
The engine consists of a single molecule as a working fluid and of course, there is a demon (a). The job of the demon is to figure out in which half of the box is the molecule located(b). Let's say the demon finds that the molecule is on the righthand side, now the demon quickly places a partition and attaches a piston on the righthand side(c). Due to the presence of molecule on the righthand side, the piston moves to the left and work is done on the load attached to the piston. Finally, the piston can be removed and the system is back to the original state(d). In this cyclic process, the engine extracts some heat energy and converts it to an equal amount of work (It can be shown that the amount of heat generated is kTln(2) ). Out of nowhere, the engine converted the thermal energy of the molecule into mechanical energy (work). The second law doesn't allow this, so one has to be wrong. Is it the second law or the Szilard's engine? You may argue that the work has to be done to insert and remove the piston. Yes, in practice work has to be done but in principle such processes can reversible and no entropy will be generated. The only option left to save the second law is again the measurement of the position of the molecule. Brillouin showed that entropy is generated to measure the position of the molecule via light signals [4]. Brillouin argued that the work generated by the engine is used to measure the position of the molecule and this is enough to save the second law. This turned out to false sigh the demon hasn't died yet. You may also wonder what's so special about the Szilard's engine? Technically, it's not much different than the original Maxwell's demon but the observations made by Szilard later turned out to be the foundation of information theory. The driving force behind the Szilard's engine is the information of the position of the molecule and the decision made by the demon is a binary operation. In a way, we can say that Szilard related information with the binary operation long before the existence of modern computers.
Finally, the last exorcism was done when R. Launder (in 1961) published his paper, Irreversibility and Heat Generation in the Computing Process [5]. Szilard had only considered the entropy generation during the measurement process but overlooked the role of memory of the demon. The Szilard's engine completes its cycle by returning to its initial state but the memory of the demon hasn't returned to its original state! The demon has to erase its memory before the next cycle begins. Launder showed that the process to erase a memory generates entropy. He also calculated the entropy generated to erase a bit of information to be k ln(2). Finally, Bennett applied this to destroy the century-old demon. Bennett (in 1973) proved that the measurement process can be reversible, so no entropy is generated in measurement[6]. Actually, the work generated by Szilard engine is employed in the memory erasure, not the measurement process. Finally, at the age of 101, the demon died. One thing to note is that although information erasure is not a reversible process, information transfer is reversible. We battled with the demon for over a century and the most important principle that we discovered from that is:
When we erase information, heat energy is generated.
Information is Physical
A striking conclusion was later by Launder in his famous statement, Information is a Physical Entity [7]. This may sound counterintuitive because we always think information as an abstract entity. His argument was that information is physical because it is always stored in a physical medium and is bound by the possible restrictions of the physical universe. We store information in a physical system, whether it is a piece of paper or a solid state drive, and the laws of physics (both classical and quantum) govern the properties of these devices, which in turn limits our capabilities for information processing. Launder himself related entropy with information, and just like entropy, information is a physical quantity that is governed by the laws of physics. The fact that information processing capabilities differ in two realms of physics, i.e. Classical and Quantum, sparkled the Quantum information theory.
Final words
Everything we have discussed so far is completely in theoretical realm but scientists have actually verified it through experiments. Back in 2010, Japanese Physicists generated energy out of information! They created their own version of Szilard's engine and using a high-speed camera (the demon), they made a molecule climb up a spiral staircase. I won't explain the working principle of their apparatus but you can read more about it here.
Maxwell would have never imagined the impact his demon made on the way we understand entropy and information. Maxwell's idea of the demon was to illustrate the statistical nature of a thermodynamic system but the demon lurked for a century to haunt generations of physicists.
References:
1. Maxwell, J. C. (1908). Theory of Heat.
2. Thomson, W. (1966). The Kinetic Theory of the Dissipation of Energy. Kinetic Theory.
3. Szilard, L. (1964). On the decrease of entropy in a thermodynamic system by the intervention of intelligent beings. Behavioral science.
4. Brillouin, L. (1951). Maxwells Demon Cannot Operate: Information and Entropy. I. Journal of Applied Physics
5. Landauer, R. (2000). Irreversibility and heat generation in the computing process. IBM Journal of Research and Development.
6. Bennett, C. H. (1982). The thermodynamics of computation—a review. International Journal of Theoretical Physics.
7. Landauer, R. (1999). Information is a physical entity. Physica A: Statistical Mechanics and its applications.
8. Bennett, C. H. (1987). Demons, engines and the second law. Scientific American.
9. Hemmo, M., & Shenker, O. R. (2012). The Road to Maxwell's Demon. Cambridge: Cambridge University Press.
10. Information Processing and Thermodynamic Entropy

SteemSTEM is a community project with the goal to promote and support Science, Technology, Engineering and Mathematics on the Steem blockchain. If you wish to support the steemSTEM project you can:
Contribute STEM content using the #steemstem tag | Support steemstem authors | Join our curation trail | Visit our Discord community | Delegate SP to steemstem