
If we know the number of bushes that a girl has cut in a given time, we can know the number of shrubs that the gardener can prune at another time. For this, we must solve a problem of proportionality that we call "Rule of three".
In the same way, questions are generated as they are in the minds of children and it is necessary to understand the importance of using this algorithm to solve simple problems of daily life, such as the example of the initial image. Solving the problem means finding the fourth term of the relationship, knowing the other three:
- Three simple rule A problem is solved with a rule of three simple when only two proportionally related magnitudes intervene. In the case of pruning of shrubs, two magnitudes intervene the number of shrubs and the hours necessary to prune them.
- The simple rule of three of direct proportionality is when the magnitudes involved are directly proportional. In the example of pruning bushes, these are directly proportional magnitudes, since the more time the gardening girl invests more bushes will prune. To solve the problem, we have the following: if in 3 hours the gardener girl has cut 15 bushes, how many bushes can the girl cut in 5 hours?

Having the following information:
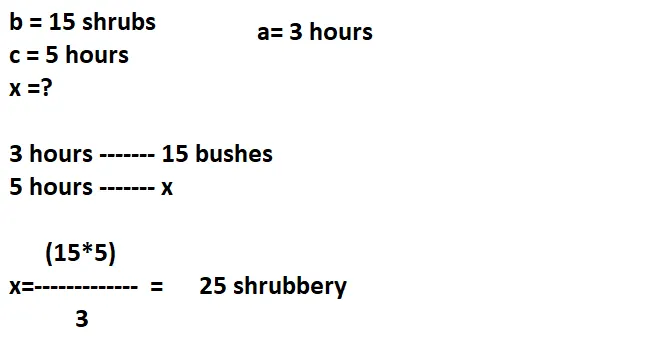
Answer: The girl gardener will trim 25 bushes in 5 hours.
- Three simple rule of inverse proportionality is when the intervening quantities are inversely proportional. In the case of a car race, the magnitudes involved are inversely proportional, since, at higher speeds, less time takes to travel the same distance.

Example:
4 people do a job in 12 days. In how many days could 6 people do the same job?
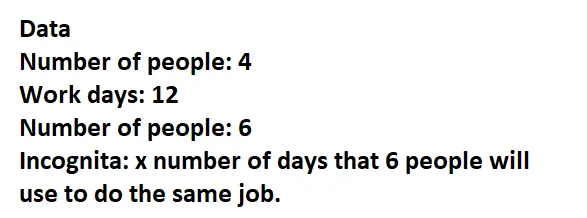


Since the signs are opposite, it means that the correspondence between the magnitudes is inversely proportional and the problem is solved forming a proportion in which antecedents are inverted and consequent of the reason in which the incognita is (x)
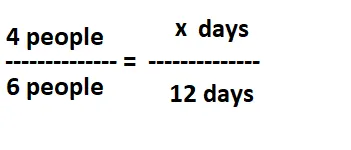
- We apply the formula to calculate a half of a proportion:

Result: 6 people will do the work in 8 days
It is important to present basic examples in classes such as the cost of refreshments, pizzas, hamburgers or articles of interest, in order to facilitate the reading comprehension of the child and also reinforces the finding of the relationship between the concepts of the problem and the way of ordering the data, since from this point is that the exact resolution of each problem is guaranteed.