
Imagen de mi pertenencia.
Uno de los factores determinantes en la calidad de un instrumento temperado es su precisión en la afinación, pues aunque esta nunca será perfecta, se puede conseguir un acercamiento suficiente para que la entonación se aprecie exacta por el oído humano. Sin embargo, esto nunca ha sido tarea sencilla, pues influyen en ello desde la altura del puente, hasta la ubicación de cada uno de los trastes, esto último ha sido un desafío especial que le ha quitado el sueño a muchos constructores de instrumentos.
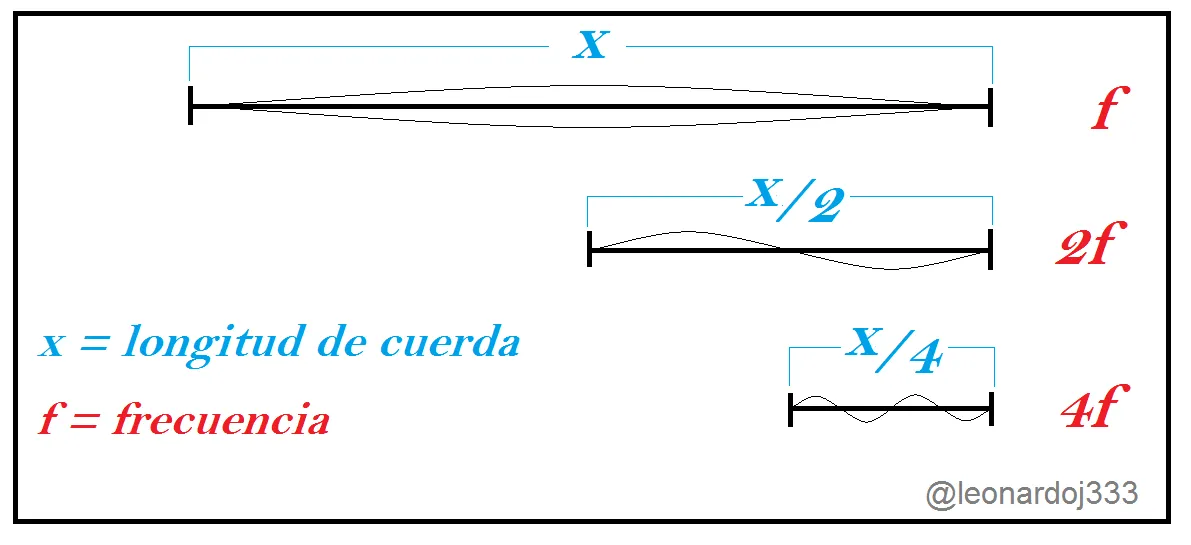
Pitágoras hizo dos aportes importantes que irónicamente generaron un problema, el primero fue la relación del tiro de cuerda vs la vibración. Podemos saber gracias a él que la frecuencia de vibración de una cuerda es inversamente proporcional a la longitud de la misma. Si es así, un segmento vibratorio cortado a la mitad vibraría al doble de la frecuencia de la primera distancia, la cuarta parte oscilaría cuatro veces más rápido y así sucesivamente .
De tal manera que conociendo la relación entre un semitono y otro y a partir de la longitud total del tiro de cuerda de un instrumento, se puede determinar la distancia exacta entre cada traste, es cuando entra en juego el segundo aporte de Pitágoras, ya que otorgó la relación de cada sonido dentro de una octava respecto a una nota inicial.
En el siguiente cuadro se podrá apreciar la relación que existe entre la frecuencia de una nota y el resto de las doce que componen un sistema temperado, tomando como referencia al Do.
Si se divide cada una de estas relaciones entre la anterior, se podrá conocer la que existe entre un semitono y otro, tal como exige la disposición común de los trastes en el sistema temperado. Sin embargo, la dificultad que se presenta es que la relación entre un semitono y otro no es una sola constante, tal como se puede observar en la siguiente imagen.
Si el cordófono constara de una sola cuerda, no habría inconveniente en disponer los trastes a partir de las relaciones anteriores, pero tratándose de una guitarra por ejemplo, que contiene seis cuerdas, surge el problema de que siendo los trastes rectos, en cada posición podrían satisfacer la afinación de una cuerda mas no de otras.

Como se aprecia en la imagen anterior, tomando como referencia la afinación tradicional de la guitarra española de seis cuerdas, las relaciones entre los semitonos dispuestos en el diapasón no son correspondientes, de tal manera que si el primer traste se ubica a una distancia en relación al número 1.067871 por ejemplo, dicha longitud daría afinación a todas las cuerdas en dicho traste a excepción de la segunda, lo mismo ocurriría en el sentido contrario para el traste dos y la misma discrepancia se encontraría a lo largo del diapasón del instrumento.
Algunos, muy pocos, constructores han resuelto el problema dividiendo cada traste en diferentes sectores a distancias distintas entre sí, uno para cada cuerda. Parecido al ejemplo siguiente.

Sin embargo, como antes se mencionó, sin necesidad de caer en tan laborioso artilugio, se puede aproximar lo suficiente a la afinación para que el defecto pase desapercibido por el oído humano. Consiste en determinar una constante que se aproxime a ambos números y con ello producir un semitono temperado.
El sistema temperado propone que la octava de una nota represente el doble de la frecuencia de la misma. Además que dicha octava esté dividida por doce sonidos a razón de semitonos. Conociendo una constante X, que al multiplicarla por la frecuencia de una nota nos arroje la de la nota correspondiente al semitono siguiente, por ejemplo al multiplicar la frecuencia de Do por X obtendríamos la frecuencia de Do#, para conocer la frecuencia de Re multiplicaríamos el resultado por X nuevamente, o bien se multiplica la frecuencia de Do por X al cuadrado. Para conocer la frecuencia de Re# se multiplicaría la frecuencia de Do por la constante elevada al cubo y así sucesivamente.

De tal forma que se puede concluir una octava de doce intervalos de semitonos multiplicando la frecuencia de una nota por la constante elevada a un exponente doce, lo que equivaldría al doble de la frecuencia de dicha nota.

De esta manera, determinamos la constante temperada, que no es más que la relación de frecuencias entre semitonos temperados, la cual además, es el intermedio entre las relaciones de los semitonos pitagóricos antes mencionados.
Cómo aplicar dicha constante al diapasón de una guitarra.
La longitud máxima de una cuerda, la cual se mide desde la cejilla del puente hasta la cejuela o traste cero, se conoce como tiro de cuerda, de su valor dependerá la distancia de cada uno de los trastes.
Para conocer el segmento correspondiente al primer traste, se divide el valor del tiro de cuerda entre la constante temperada, el resultado será la distancia entre la cejilla del puente y el traste uno, la cual equivale al sector vibratorio que proporcionará el semitono siguiente. Para conocer el valor del segmento correspondiente al traste dos, se divide el tiro de cuerda entre la constante elevada al cuadrado, y así sucesivamente variando la potencia de la constante según el traste o el segmento que se esté determinando.

En el ejemplo anterior se determinó el valor del traste uno seguido del dos, a partir de un tiro de cuerda de 580mm normalmente usado en cuatros de 17 trastes. Las demás distancias acotadas se determinaron de la diferencia entre el tiro de cuerda y los resultados obtenidos.
Todos estos cálculos se pueden programar en una hoja Excel por ejemplo, de tal manera que al introducir la longitud de un determinado tiro de cuerda, el programa arroje todos los valores correspondientes a cada traste, de forma automática.
Para finalizar, debo confesar que en mi ejercicio como luthier, he podido ver trabajos de artesanos que se han formado empíricamente, por lo que carecen de los conocimientos técnicos del presente artículo, pero que a pesar de ello, sorprendentemente han conseguido brindar una afinación aceptable en sus instrumentos, con medidas y proporciones que no se parecen a las mundialmente utilizadas y expuestas en este artículo, por lo que me atrevo a decir que no sería el único método para temperar correctamente un instrumento.


