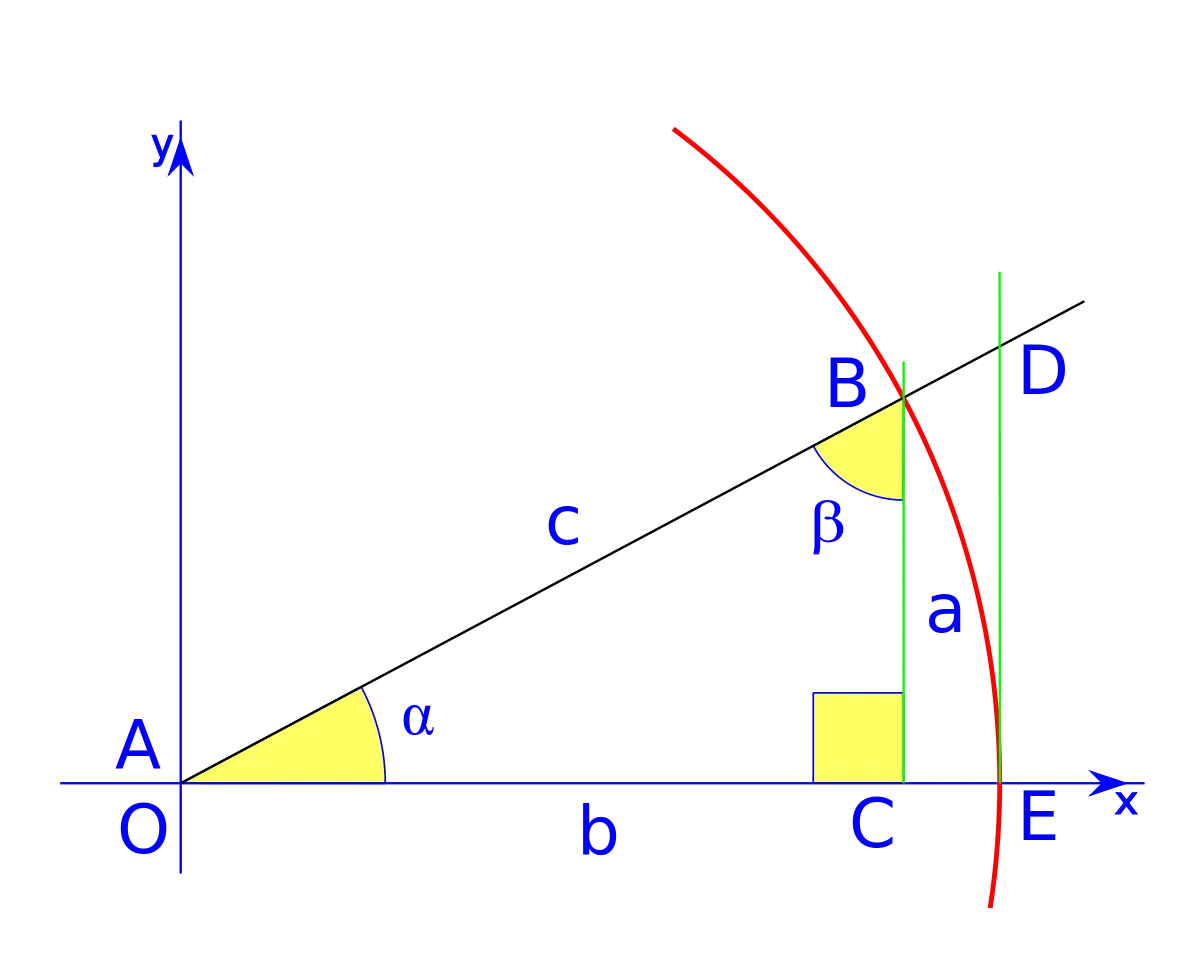
Definición y objeto
Como es muy conocido, por geometría básica, cuando se trata de construir una figura poligonal no es necesario conocer, o que se den, todos los elementos de aquella, sino que hay en dicha figura cierto número de ellos que vienen determinados por el conocimiento de otros elementos de la misma: así, por ejemplo, para construir un triángulo, basta que se den sus tres lados, o dos lados y ángulo comprendido entre ellos, o dos lados y ángulo, etc.
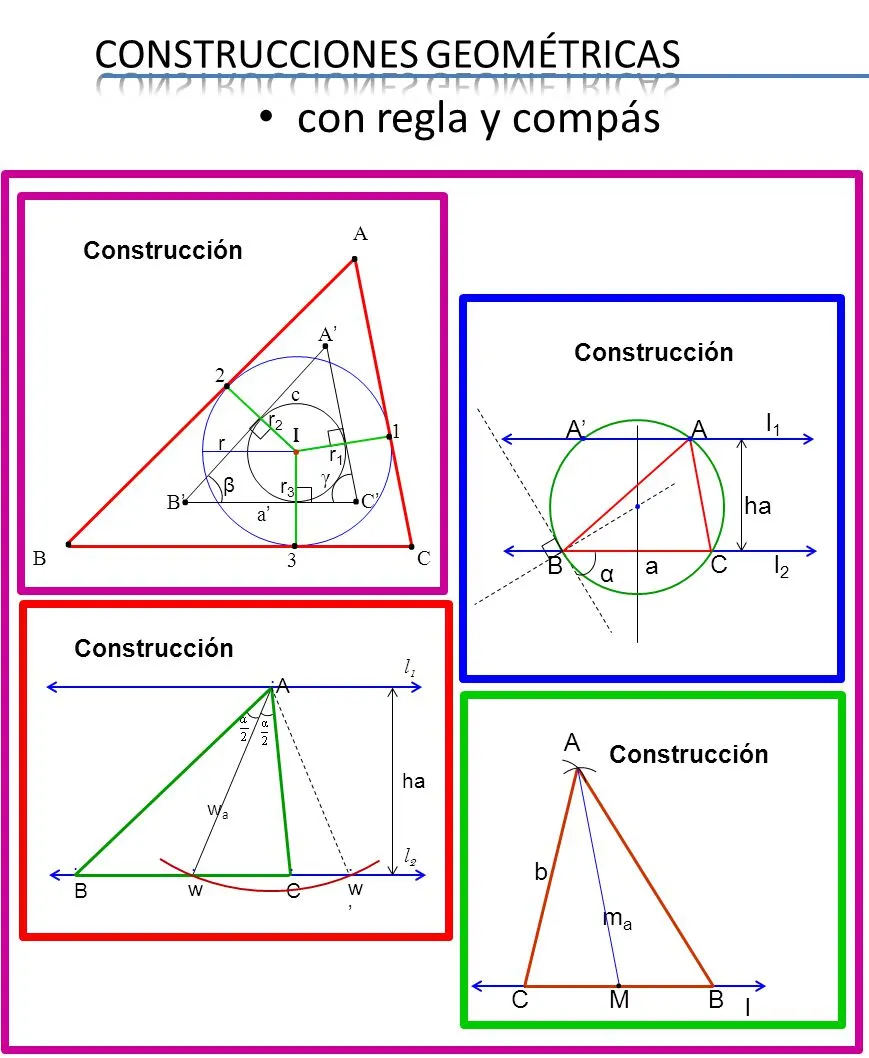
De igual manera, para construir un paralelogramo basta que se den dos lados y el ángulo comprendido, o dos lados contiguos y una diagonal, etc. Una vez construidas las figuras, en cualquiera de los dos casos referidos, quedarían determinados todos los elementos desconocidos de cada una de ellas. Ahora bien, la imperfección de los instrumentos que se hayan podido utilizar, el grosor de las líneas, y lo defectuoso que pudieran resultar nuestros sentidos, son todas circunstancias que influyen para que los resultados, de la construcción, no sean exactos, sino aproximados, lo que da pie a pensar en las ventajas que puede proporcional calcular los elementos desconocidos en lugar de intentar determinarlos por construcción.

En este contexto, La Trigonometría, disciplina matemática de la que trataremos a continuación, suministra estos procesos de cálculo para que la medición de magnitudes angulares sea posible con la precisión que se quiera, de modo que enseña los medios para encontrar por simples cálculos ciertos elementos de una figura cuando son conocidos los demás, lo cual significa resolver la figura.
Ahora bien, como la Geometría gira en torno a al triángulo ya que todas las demás figuras poligonales, por complicadas que sean, pueden ser reducidas a triángulos, la Trigonometría se dedica, en especial, a la reducción de triángulos.
En síntesis, podemos decir, que : La Trigonometría es la parte de las Matemáticas que, valiéndose del cálculo, resuelve triángulos; o sea, calcula los desconocidos de los mismos cuando se dan los datos suficientes para que la figura quede determinada.
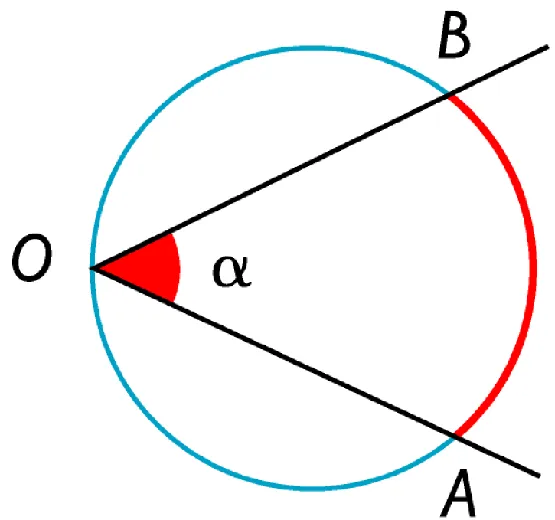
Sistemas de medidas de ángulos y arcos
Como bien es conocido, medir un ángulo significa compararlo con otro ángulo que adopta como unidad de medida. De manera similar, medir un arco de circunferencia significa compararlo con otro arco de la misma circunferencia, o de otra de igual radio, que se adopta como unidad de medida.
Por otra parte, conviene recordar, en este punto, que de la proporcionalidad que existe entre los ángulos centrales y sus arcos correspondientes, se deduce: la medida de un angulo central es igual a la del arco correspondiente, tomando como unidad de arco, al arco que abarca la unidad de ángulo.
Comúnmente se emplean en Trigonometría dos unidades de medidas distintas para la comparar ángulos, a saber: Sistema Sexagesimal y el Sistema Circular o Radián. Hoy les comparto alguna pequeña descripción del primero de los sistemas referidos, esperando recordarles su paso por el segundo año de bachillerato cuando les hablaban , por primera vez, del sistema sexagesimal.
El sistema sexagesimal
El ángulo elegido como unidad de medida puede ser cualquiera. En el sistema sexagesimal, la Geometría adopta omo unidad principal de ángulo al grado sexagesimal, que es la 90ª parte del ángulo recto, y como unidades secundarias, al minuto sexagesimal que es la 60ª parte del grado, y al segundo sexagesimal que es la 60ª parte del minuto; partiendo de esto, las unidades sexagesimales de arco son, entonces, los arcos de circunferencia que abarcan los ángulos centrales respectivos de un grado, de un minuto y de un segundo sexagesimal.
En símbolos, estas relaciones se expresan del siguiente modo:
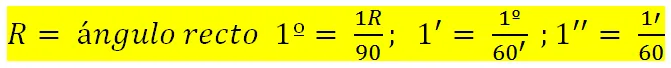
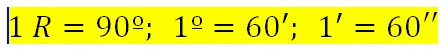
A su vez,los segundos se dividen en décimas, centésimas, etc., de manera que para expresar, por ejemplo, que un ángulo mide 72 grados, 32 minutos, 18 segundos y 25 centésimas, sexagesimales, escribimos:
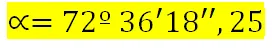
Hasta acá, por el día de hoy, nuestro trigonométrico recorrido, seguimos en contacto.