Hola amig@s, bievenidos a nuestro acostumbrado encuentro. Hoy, para darle continuidad a nuestro post anterior De los naturales a los complejos, les invito a al mundo de la resta, la división y la potenciación en los naturales.
La resta o sustracción en N

Es decir, que diremos que a – b = c, si ocurre que b + c = a. Por ejemplo, decimos que 11 – 8 = 3 porque 3 es número que hay que sumar a 8 para obtener 11.
Diviisión en N

O sea, que diremos que D/d = c siempre que d . c = D. Por ejemplo, decimos que 24/ 3 = 8 puesto que 8 es el número que hay que multiplicar por 3 para obtener 24.
La idea de división de números naturales es la de reparto. Así, la división de 100 : 5 = 20, se interpreta como un reparto de 100 elementos (dividendo) entre 5 partes (divisor), de modo que a cada parte le corresponden 20 (cociente).
Cuando con el reparto acabamos con todos los elementos disponibles, como el caso del ejemplo, la división se llama exacta.
Cuando no es disponible un repearto exacto y sobran algunos elementos, la división se llama entera (o inexacta). En ella, además de un cociente, se obtiene un resto, según el siguiente algoritmo:
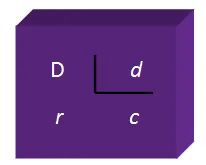
La relación fundamental de cualquier división es conocida como “prueba de la división” que dice:


Si tenemos la siguiente divisón: 135 : 8. Utilizando el algoritmo de la división tenemos:
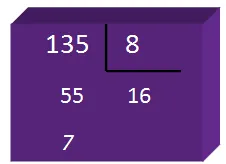
Donde: 135 = 8 . 16 + 7
Potenciación en N
La potencia natural de un número natural no es más que una multiplicación reiterada. Así, cuando decimos “a elevada n” tenemos:

Al número “a” se le llama base de la potencia, mientras que a “n” se le llama exponente de la potencia.


Propiedades de la potenciación en N
La potenciación, definida en el conjunto de los números naturales, verifica las siguiente propiedades:


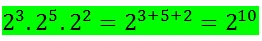


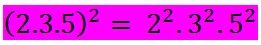



Con esto hemos llegado al final de nuestro recorrido por el conjunto de los números naturales. En un próximo viaje nos embarcaremos con rumbo al conjunto de los números enteros, les espero en esa próxima oportunidad.
...Hasta la vista amigos!!