Así hablamos, en la publicaciones anterior, divisibilidad, de los números primos y compuesto , como también de los criterios de divisibilidad. Siguiendo con esos fundamentos previos hoy le corresponde el turno a lo que seguramente recuerdan haber trabajado en su escuela básica, nos referimos al Mínimo Común Múltiplo (m.c.m) y al Máximo Común Divisor (M.C.D).
Antes de entrar, de lleno, a los aspectos anteriores recordemos la descomposición en factores primos.

Descomposición en factores primos

Para ello, se divide el número por el menor de sus divisores que sea un número primo. Luego, el cociente obtenido se vuelve a dividir por el menor de sus divisores que sea, igualmente, un número primo y así sucesivamente hasta obtener como cociente un número que sea primo.

Descomponer en factores primos 37.800:

Por lo tanto, podemos escribir 37.800 como un producto de factores primos de la forma siguiente:

Mínimo Cómún Múltiplo

Así, el mínimo común múltiplo, por ejemplo, de 6, 8 y 10 es 120, pues 120 es el menor múltiplo común de 6, 8 y 10, respectivamente.
Cómo determinar el m.c.m
Para determinar el mínimo común múltiplo entre varios número dados, simplemente descomponemos dichos números en sus factores primos y de dichos factores tomamos los comunes y no comunes con su mayor exponente. Formamos un producto con la selección realizada y el resultado será el m.c.m buscado.

Tomemos como ejemplo los tres números anteriores, 6, 8 y 10 y verifiquemos que el m.c.m es 120 aplicando, ahora, el procedimiento descrito.
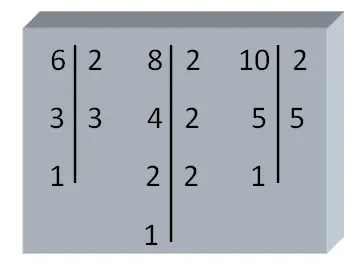
Entonces:
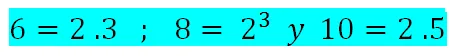
Tomando, ahora, los factores comunes y no comunes elevados al mayor exponente, resulta:
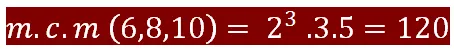
Máximo Cómún Divisor

Así, por ejemplo, si consideraos, nuevamente, los números 6, 8 y 10, tenemos que el M.C.D, entre dichos números es 2, pues es el 2 el mayor divisor común existente entre 6, 8 y 10.
Cómo determinar el M.C.D
Para determinar el máximo común divisor entre varios números, descomponemos dichos números en sus factores primos. De dichos factores seleccionamos solamente los factores comunes y el producto de dichos factores será el M.C.D buscado.

Tomemos, nuevamente, como ejemplo los tres números anteriores, 6, 8 y 10 y verifiquemos que el M.C.D es 2 aplicando, ahora, el procedimiento antes descrito.

Entonces:
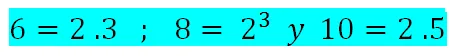
Luego, al seleccionar los factores comunes, con el menor exponente, resulta:

Nótese, que solamente el 2 un factor común entre los tres números seleccionados y sólo debemos considera el de menor exponente, como ya lo habíamos resaltado.
Bueno amigos, hasta acá nuestra publicación del día. Ahora, ya estamos preparados para, en nuestra próxima publicación, empezar conocer debidamente al conjunto de los números racionales.
...Hasta entonces!!