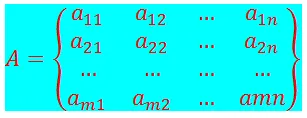
Introducción histórica
El desarrollo del álgebra linea se alcanza en el siglo XIX gracias sobre todo a los trabajos de los matemáticos británicos Joseph Sylvester y Arthur Cayley. A Sylvester se debe, en 1850, la denominación de matriz para disposición rectangular de números actual, y a Cayley, en 1855, el descubrimiento de la conexión entre el cambio lineal de variables en un sistema y la noción de producto de matrices.
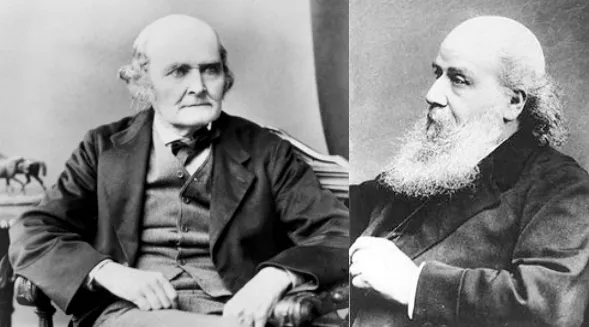
Matrices: Definición
 !
!El primer subíndice de cada término de la matriz indica filas y el segundo columnas. Así, el término a31 es el que se encuentra en la fila 3 y la columna 1. En general, aij es el término situado en la fila i y la columna j.
Cuando nos interese referirnos a la matriz sin escribir la tablas, simplemente escribimos:

Ejemplos:
1.-

Es una matriz de orden 4x4 (4 filas y 4 columnas) en la cual a13=a34=4; a41=0, etc.
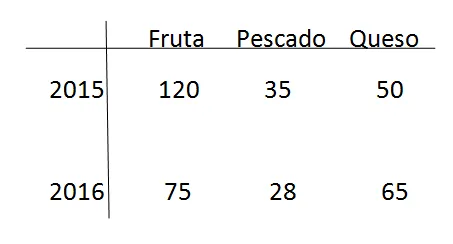
2.- El consumo de en kilos de frutas, pescado y queso de una familia durante el 2015 y el 2016 se puede disponer en forma de matriz de la manera siguiente:
Tipos de matrices
Al estudiar las matrices es conveniente reconocer algunos tipos especiales de matrices. Algunos de estas matrices especiales son las siguientes:

Ejemplo:

Es una matriz de orden 1x4

Ejemplo:
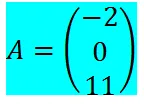
Es una matriz de orde 3x1

Ejemplo:
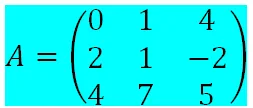
Es una matriz de orden 3x3

Ejemplo:
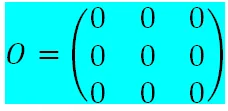
Diagonal principal de una matriz: es el conjunto de elementos de la forma aii,
Ejemplo:
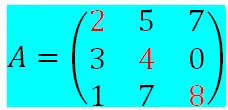
La diagonal principal está formada por los elementos 2, 4, 8. En todos ellos el subíndice que indica la fila y la columna es el mismo.

Ejemplo:
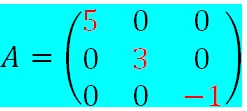

Ejemplo:
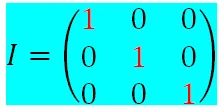

Ejemplo:
1.-

Triangular superior
2.-

Triangular inferior
Bueno amig@s, hasta acá este primer post relacionado a las matrices. Les prometo una segunda publicación donde trataremos lo relativo a las operaciones con las matrices.
Hasta un próximo encuentro