En el post anterior, Hablemos de las funciones en matemáticas, referíamos una aproximación conceptual, y una definición formal, respecto al contenido de la funciones.
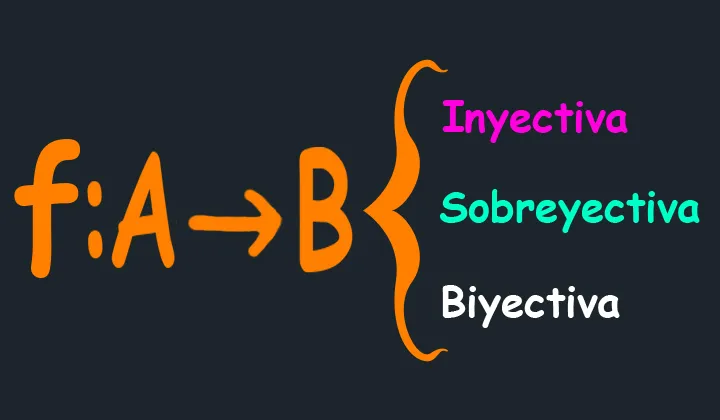
Clasificación de las funciones
Luego de la definición de función, que indicábamos en nuestra publicación anterior, queda claro que toda relación función es una relación, pero no toda relación es una función, las Condiciones de Existencia de imagen y Unicidad de imagen determinan, en esencia, el grado necesario para que una relación sea, efectivamente, una función. Ahora bien, centrándonos en aquellas relaciones que alcanzan el estatus de función, podemos clasificar a éstas en uno de tres tipos conocidos, a saber: Inyectiva, Sobreyectiva o Biyectiva.
Función Inyectiva
Una función f, de un conjunto A en otro conjunto B, diremos que es inyectiva si, y sólo si, cada par de elementos diferentes del conjunto de partida A, tienen imágenes diferentes en el conjunto de llegada B.
Simbólicamente:
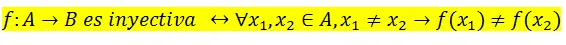

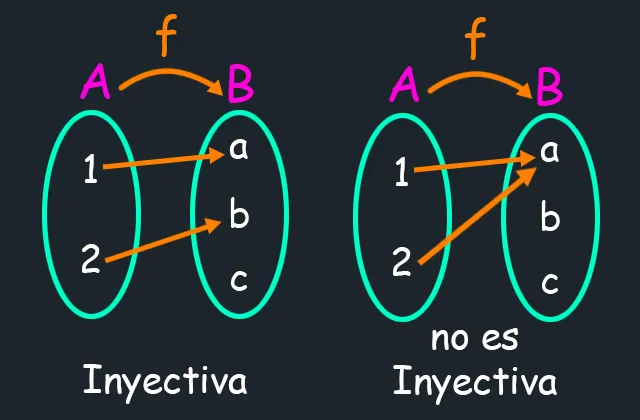
Nótese que en el primer ejemplo, a la izquierda, "elementos distintos tienen imágenes distintas", por lo tanto la función es inyectiva. Contrariamente, en el segundo ejemplo, dos elementos distintos del conjunto de partida tienen una misma imagen, en tanto, esa función no es inyectiva.
Función sobreyectiva
Una función f, de un conjunto A en otro conjunto B, es sobreyectiva si cada uno de los elementos "y" del conjunto de llegada B, es imagen de al menos un elemento "x" de A.
En símbolos
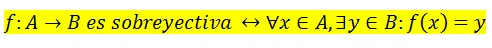

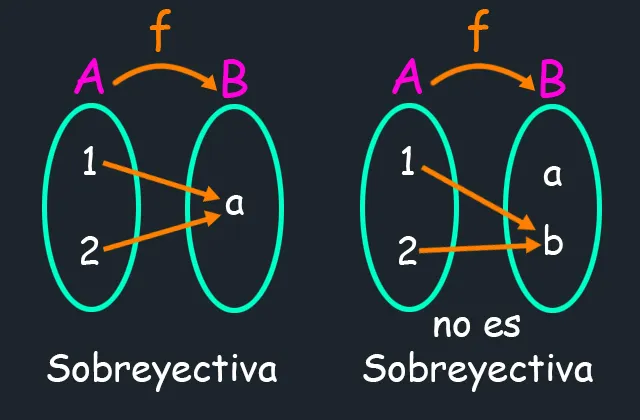
Pueden observar amigos, que en el primer caso todo el conjunto B es imagen, no importa que sea un sólo elemento, así fuesen más todos deberían ser imágenes para que la función sea sobreyectiva. En el segundo ejemplo, a la derecha, se puede observar que no todos los elementos del conjunto de llegada son imágenes, por lo tanto, la función no es sobreyectiva.
Función Biyectiva
Una función es biyectiva cuando es inyectiva y sobreyectiva a la vez

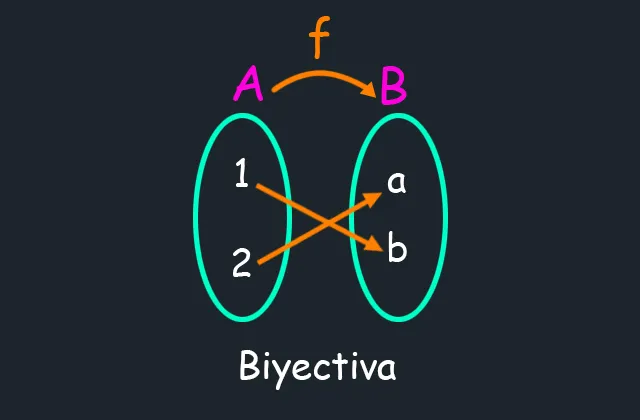
Se puede apreciar que elementos distintos del conjunto de partida tienen imágenes distinta, por lo tanto la función es inyectiva. Adicionalmente, todo el conjunto de llegada es imagen, por lo que la función es sobreyectiva, entonces, al ser la función inyectiva y sobreyectiva, también biyectiva.
Función como fórmula general
La definición de una función es la regla de correspondencia a través de la cual se asocian los elementos del conjunto de partida con sus correspondientes imágenes, en el conjunto de llegada.
En matemática, generalmente, las funciones se expresan mediante una fórmula general como una forma de sustituir el lenguaje ordinario por otro de tipo formal o propiamente matemático.

Sean los conjuntos:
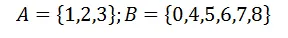
y la función:
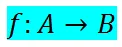
definida como f(x)= x+3. Las imágenes de cada x de A, se obtiene evaluando las mismas a partir de la definición o fómula.
Así:
f(1)=1+3= 4, es decir, la imagen de 1 es 4
f(2)=2+3=5, la imagen de 2 es 5
f(3)=3+3=6, la imagen de 3 es 6
Bueno amig@s hasta mi post del día, te invito a que indiques en los comentarios el tipo de función que resultó en el ejemplo anterior. De igual manera, si te interesa algún contenido, en particular, no dudes en solicitarlo. Saludos