Hola amig@s, bienvenidos a un nuevo encuentro con el fascinante mundo matemático donde trataremos, en esta oportunidad, el importantísimo aspecto de las "funciones". En mi post anterior El Sistema de los Números Naturales, les prometía que les traería un contenido relativo a las funciones por la importancia que revestía esa información para la mejor comprensión respecto al Sistema de lo números Naturales. Pues bien, comencemos a cumplir con lo prometido.
Qué es una función
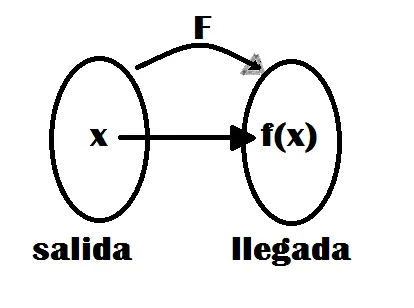
Inicialmente, como si se tratara de la explicación a joven de 13 o 14 años, pensemos en una función como un tipo particular de relación. Si, toda función es, en esencia, una relación que se da entre los elementos de dos conjuntos, que llamaremos , genéricamente, conjunto A y conjunto B, conjuntos de llegada y de partida, respectivamente. Los elementos de estos conjuntos pueden ser de cualquier naturaleza: personas, animales, libros, letras, símbolos, números, etc, etc.
La particularidad de las funciones, dentro del mundo de las relaciones, radica en el hecho que para ser efectivamente una función la relación, entre los elementos de los conjuntos considerados, debe cumplir con la condición que todo elemento del conjunto A, llamado de partida, debe estar asociado con uno, y sólo un, elemento del conjunto B, llamado de llegada. Por ejemplo, pensemos en conjunto A, de partida, formado por las personas en la cola de la entrada a un cine y, tenemos un conjunto B, de llegada, formado por las butacas al interior del cine. A partir de estos dos conjuntos se podría establecer una función cuya definición de asociación podría ser algo así como: "lugar de ubicación en la sala del cine". Es de suponerse que cada persona en la cola, Conjunto de Partida, tendrá derecho a una butaca , pero ponemos el énfasis a que sólo podrá tener una sola butaca, nadie del conjunto del las personas podría estar usando dos butacas, por lo que una relación en el caso descrito cumple con la condición para ser considerada como una función.
En este punto, podemos ahora enunciar el concepto, luego daremos la definición formal, de lo que es matemáticamente una función:
"Llamaremos función de un Conjunto A, llamado de partida, en otro conjunto B, llamado de llegada, a toda relación que asocia a cada elemento "x" del conjunto de partida un único elemento "y", del conjunto de llegada"
Una función "f" de un conjunto A en otro conjunto B, la representamos :
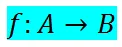
Si elemento x de A , está asociado con un elemento y de B, mediante la función f, escribimos:
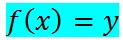
y decimos que "y es imagen de x, mediante la función f".
Ejemplo:
Sean dos conjuntos:

En ellos se define la función f de la manera siguiente: "pertenece al aparato". por lo que resulta, lo siguiente:
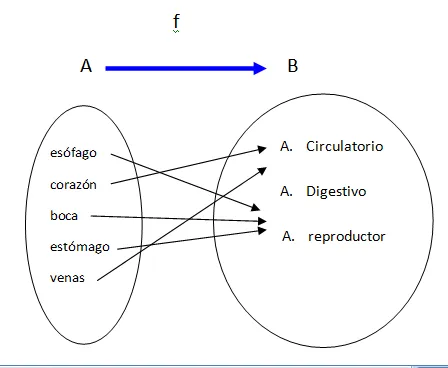
Podemos decir, entre otras, que :
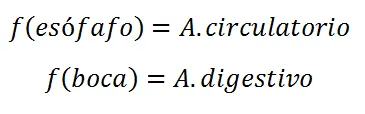
Anímate a encontrar el resto de correspondencias.
Nótese que la imagen de "esófago y corazón" es la misma, así como "A. digestivo" es la imagen de 3 elementos de A, eso para nada contradice la idea de función que se ha expuesto , puesto que todos los elementos del conjunto de partida tienen imagen correspondiente y esa única para cada elemento, sin importar que sea la misma para algunos de ellos. Tampoco debe importarnos, que algún elemento, o varios de ellos, perteneciente al conjunto de llegada no sea imagen de algún elemento "x" del conjunto de partida, nótese, por ejemplo, que "A. reproductor" no es imagen de ningún elemento del conjunto A.
Definición formal
El concepto de función, que hasta acá hemos descrito, lo podemos expresar mediante una definición formal, desde el álgebra moderna , y al nivel del pre-grado universitario, de la manera siguiente:
Sean los conjuntos A y B, no vacíos, la relación R, subconjunto del producto cartesiano AxB es una función de A en B que se simboliza
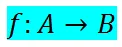
si sólo si satisface las dos siguientes condiciones:
a) Condición de existencia

b) Condición de unicidad
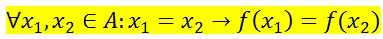
Leyenda:

Buenos amig@s hasta el post de hoy, complentaremos este contenido con una publicación dedicada a la clasificación de las funciones. Hasta entonces!!