Ya hemos conocido un contenido importante respecto a los Naturales y los Enteros, en la secuencia perfecta le tocaría el turno a los Racionales, a las fracciones. Sin embargo, para avanza correctamente sobre el conocimiento de los racionales , resulta conveniente que antes conozcamos algunos aspecto íntimamente relacionados con las operaciones con las fracciones.
En este sentido, abriremos un compás sobre los conjuntos numéricos y trataremos, primeramente, lo relacionado con la divisibilidad lo cual resultará muy provechoso, y fundamental, para operar debidamente en el conjunto de los números racionales. Iniciemos!!
Introducción Histórica: Criterios de divisibilidad
La divisibilidad de los números es conocida desde tiempos remotos. Así, los hindúes ya conocían la divisibilidad por tres, siete y nueve y los egipcios conocían los números pares e impares. El matemático griego Euclides demostró, por su parte, los teoremas básicos de la divisibilidad de números enteros, Ya posteriormente, el matemático francés Pascal (1623- 1662) propuso las reglas para conocer la divisibilidad de cualquier número.

Números primos y compuestos
Un par de definiciones muy importantes respecto a la divisibilidad son las referidas a los números primos y los números compuestos.

Así, por ejemplo, 3 es un número primo ya que sólo lo pueden dividir, exactamente, el mismo 3 y la unidad (1). De igual modo, 13 es un número primo pues sólo lo dividen el 1 y el mismo 13.
A continuación, una tabla de los primeros, resaltados en naranja, considerando los primeros 100 números naturales:
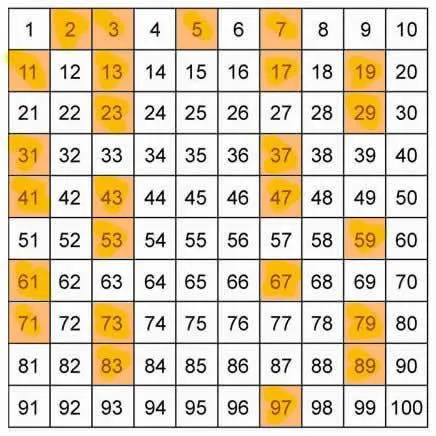

Tenemos, como ejemplos de números compuesto el 6, que lo dividen además del 1 y el mismo 6, el 2 y 3. De igual modo, son ejemplos de números compuestos el 4, el 8, el 10, etc. En todos esos casos, siempre tendremos más de dos divisores para el número dado.
Múltiplos y divisores

Así, por ejemplo, el número 18 es múltiplo de de 6 puesto que lo contiene exactamente 3 veces. En este sentido, de igual modo, decimos que 18 es divisible por 6.
Por otra parte:

Así, por ejemplo, 5 es divisor de 20 por que ésta contenido exactamente 5 veces en 20
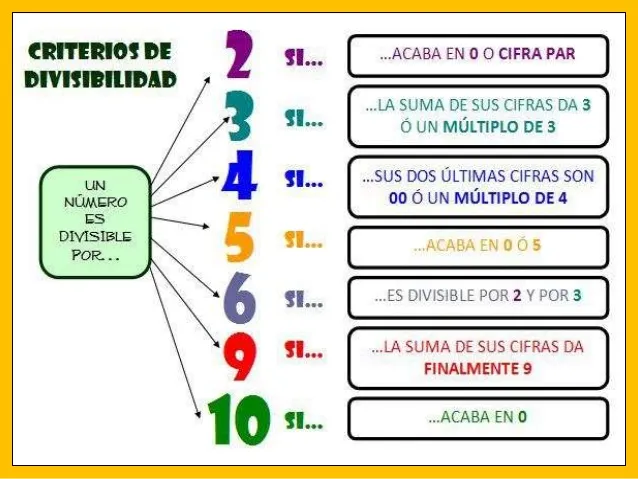
Criterios de divisibilidad
Los criterios de divisibilidad son señales características de los números que permiten conocer cuáles son sus divisores. Son muchos los criterios de divisibilidad conocidos, sin embargo, para efectos prácticos acá sólo describiremos los más comunes o más empleados, a saber: criterios de divisibilidad por 2, 3 y 5.
Divisibilidad por 2 : un número es divisible por 2 cuando termina en 0 o en cifra par.
Así `por ejemplo son divisibles por 2 números como: 4, 46, 78, 100, 50, 36, etc.
Divisibilidad por 3 : Un número es divisible por 3 cuando la suma de sus dígito es múltiplo de 3.
Así 48, es divisible por 3, puesto que si sumamos los dígitos que conforman 48, esto es, 4 + 8 = 12 y 12 es múltiplo de 3.
De manera análoga podemos decir que son divisibles entre 3 números como: 18, 21, 30, 66, 93, etc. En cada caso, la suma de los dígitos de las números anteriores son múltiplos de 3.
Divisibilidad por 5 : un número es divisible por 5 cuando terminan en 5 o en 0. Así, por ejemplo, son divisibles por 5 números como: 55, 35, 70, 805, 700, etc.
Hemos llegado al final de nuestra publicación del día. Les invito a un nuevo encuentro donde la matemática y steemit se conjugaran para darles la más cordial bienvenida. Hasta próxima!!