En las dos publicaciones anteriores tratábamos lo relativo al conjunto de los números naturales, aquellos que resaltábamos como los números que utilizamos para contar. Cuando este conjunto, los naturales, se agota y son necesarias algunas operaciones más complejas, en el campo de la matemática, la primera puerta que se abre son la de los números enteros, sobre este conjunto dedicaremos hoy nuestro contenido. Acompáñenme!!
Por qué aparecen los enteros. Introducción histórica
La primera consideración histórica que se tiene sobre el número negativo no llega al mundo occidental sino hasta el siglo XVI como consecuencia de la solución de ecuaciones algebraicas que resultan irresolubles en el campo de los naturales. Piensen, por ejemplo, en la imposibilidad de resolver una ecuación como x + 3 = 1. Lo anterior, resulta, evidentemente, imposible en N, puesto que no existe ningún natural que sumado a 3 de como resultado el número 1.
Sin embargo, en Oriente, mucho antes que en Occidente, en el siglo IV ya se manipulaban números positivos y negativos haciendo uso de los ábacos constituidos por bolas de diferentes colores.
Los enteros al auxilio de los naturales
Una dificultad que presenta el conjunto de los números naturales es que la resta o la división de un par de números naturales puede dar como resultado otro número que no sea natural. Así, por ejemplo, 7 -11 no es una operación que esté definida en el conjunto N, pues el resultado no es un número natural, lo mismo sucede con la división de 5 : 2, cuyo resultado no será un número natural.
Ante la anterior dificultad, los enteros salen al auxilio de los naturales. En este sentido, ampliamos el conjunto N a otro más grande que llamaremos Conjunto de lo Números Enteros, que denotamos con la letra “Z”, y que definimos en los siguientes términos:

Al poder contar con los números negativos, adicionales a los naturales, el conjunto Z nos permite, además de sumar y multiplicar, poder restar con la seguridad que el resultado siempre será también un número entero.
Representación gráfica
Cuando referíamos la representación gráfica de los naturales se decía que utilizaríamos un segmento recta que se extendía infinitamente hacia la derecha, indicado por una punta de flecha en ese extremo, por ser un conjunto infinito, es decir, que crecía infinitamente a medida que avanzamos a la derecha.
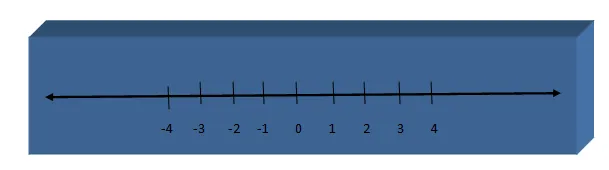
Los enteros son un conjunto infinito, tanto a la derecha como a la izquierda, por ello lo representamos a través de una recta con punta de flecha en ambos extremos, tal como se aprecia:
Valor Absoluto
Para realizar las operaciones con los números enteros primero debe introducirse una definición muy importante, nos referimos a lo que tiene que ver con el valor absoluto, entendido como:

Desde el punto de vista analítico, en la práctica, el valor absoluto de un número entero es igual al mismo número prescindiendo del signo.


¿Quién va primero?
El conjunto Z, a igual que N, es un conjunto ordenado. En este sentido, dados dos o más números enteros lo podemos ordenar, de menor a mayor, o viceversa; siguiendo una simple regla que se describe a continuación.


Dados los números enteros 5, -21 y 0. Si los ordenamos de menor a mayor tendríamos la siguiente secuencia:
-21, 0,5 puesto que -21 es menor que 0 y 0 a su vez 0 es menor que 5, es decir: -21<0<5
Si el orden fuera de mayor a menor la secuencia sería entonces: 5, 0, -21 , ya que 5>0>-21
Hasta acá nuestro post del día. En una próxima entrega les compartiré las operaiones en el conjunto de los números enteros.
Les invito a que me acompañen en mi próxima publicación. Hasta entonces!!