Seguramente muchos de vosotros os habréis preguntado por qué un folio tiene tamaño DIN A4 o qué significa eso de DIN A4.

Se llaman así porque forman parte de una serie de tamaños: A0, A1, A2 ... A8 y cada uno es la mitad del anterior.
El papel DIN A0 mide 1 m2
El papel DIN A1 mide la mitad 1/2 m2
El papel DIN A2 mide la mitad del anterior 1/4 m2
Y así sucesivamente
Estos papeles están pensados para poder aumentar y reducir su contenido sin que se deforme, es decir, si llevas un dibujo, por ejemplo, en un papel DIN A4, se podrá aumentar sin problemas a tamaño A3, A2 ... o reducir a tamaño A5, A6 ... sin que se deforme porque las proporciones son las mismas.
Siguiente la imagen anterior, vamos a comprobarlo:
El DIN A0 mide 1189 mm de alto por 841 mm de ancho.
Si dividimos 1189 / 841 = 1.41379310345
El DIN A1 mide 841 mm de alto por 594 mm de ancho.
Si dividimos 841 / 594 = 1.41582491582
...
El DIN A4 mide 297 mm de alto por 210 mm de ancho.
Si dividimos 297 / 210 = 1.41428571429
Como podéis comprobar, el resultado siempre es el mismo, variando simplemente en milésimas, algo despreciable para este caso. Pero, ¿no os suena de algo el resultado de estas proporciones? Pues sí, es equivalente a la √2.
√2 = 1.41421356237
Esto se puede demostrar de una manera muy sencilla. Tengamos en cuenta el dibujo siguiente.
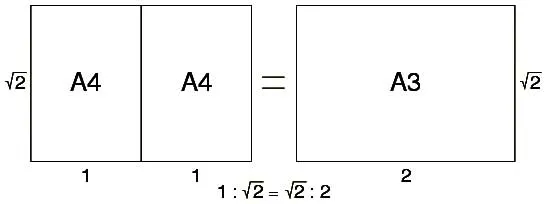
Si partimos de A3 con ancho A y alto B, al crear un A4 lo que ocurre es que su ancho sería B y su alto A / 2.
Entonces, lo que nosotros queremos es:
A / B = B / (A / 2)
A / B = 2B / A
A * A / B * B = 2
A2 / B2 = 2
Aplicando √ a ambos lados
A / B = √2
