Leonhard Euler (1707-1783 ), fuente de imagen de dominio de wikimedia commons.
Cuando hablamos de grafos, hacemos referencia de Leonhard Euler, matemático, físico y filósofo suizo, fue quien realizó grandes avances en la teoría de grafos, lo más fascinante para poder llegar a esta teoría, el número de Euler (e), como una constante, que el valor de la derivada está representada por la pendiente de la línea tangente, de la función f ( x )= e^x, de tal manera cuando el valor de x= 0 esta es igual 1, hasta considerar logaritmo natural o logaritmo en base e, teniendo base de soporte en este logaritmo, desarrollo la teoría de grafos o teoría de las gráficas, basando se en el análisis de las propiedades de los grafos o gráficas. Donde un grafo es un conjunto, no vacío de vértices o nodos y una selección de pares de vértices, el cual son aristas, considerando lo siguiente, que pueden ser orientados o no, de tal manera, que un grafo se representa mediante una serie de puntos ,en este casos serían los vértices, al mismo tiempo están conectados por líneas de las aristas.
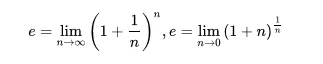
Fuente de imagen de dominio de wikimedia commons.
Este gran aporte sirvió de base fundamental, para el análisis y definición de las funciones logarítmicas y exponenciales, luego de su trabajo de la teoría de los grafos, también descubrió el teorema de la composición de integrales elípticas, dando como resultado le dios más perfección a la geometría plana y de sólidos. Es por eso, que entre las estructuras más sencillas y usadas se encuentran las listas y las matrices, aunque frecuentemente se usa una combinación de ambas en los grafos, ya que a la teoría de grafos no le interesa saber, qué son los vértices, la forma de las aristas no son relevantes, sólo importa a qué vértices están unidas.

Los grafos son el objeto de estudio de esta rama de las matemáticas, el grafo pez, fuente de imagen de dominio de wikimedia commons.
Pero también existe el caso, que si existe una única arista e asociada con el par ordenado (v, w) de vértices, escribimos e = (v, w), lo cual denota una arista de v a w, se afirmar, que un grafo dirigido es aquel, que tiene uniones unidireccionales. Hay que tomar en cuenta lo siguiente para entender un poco más sobre este contenido, existen vértices adyacentes, que conforman un lado o arista, en donde todos los lados conformado por dos vértices, se dice que es incidente sobre esos vértices, si un vértice no tiene otro adyacente se dice que es aislado, gracias a ello al momento de graficar, los diagramas de los grafos, se pueden representar gráficamente cuando la cantidad de vértices no es grande, porque también permite el caso, que dos grafos son isomorfos, si existe correspondencia uno a uno entre los nodos de ambos grafos, y además conservan la adyacencia tanto entre los nodos como en la dirección de los lados, por medio del modelo matemático definido, G1 = (V1, E1) y G2 = (V2, E2) grafos simples, se dice G1 y G2 son isomorfos de la misma forma, si hay una función biyectiva f de V1 a V2, con la propiedad de que a y b, son adyacentes en G1 si y solo si f(a) y f (b), son adyacentes en G2, para todo a y b en V1 tal función f, es llamada un isomorfismo.
Entiendo que es un poco complicado, por el manejo técnico de este modelo matemático, pero su aplicación es muy diversa mi amigos lectores, tales como: sirvió de uso del pandeo de soportes verticales y generó una nueva rama de ingeniería con sus trabajos sobre la carga crítica de las columnas, en la actualidad nos sirve, para diseñar redes, dentro de la programación para el diseño de circuitos, cartografía en el coloreado de mapas, ciencias sociales, ciencias físicas, ingeniería de comunicación, es una amplia gama de uso de este modelo matemático caracterizado por lógica de diseño y gráficos.
En la filosofía tenía la siguiente postura, insistía en que el conocimiento se basa en parte, en la existencia de leyes cuantitativas precisas, algo que el monismo y las teorías filosóficas de Christian Wolff, no eran capaces de proveer, Ya que el desarrollo del cálculo era una de las cuestiones principales de la investigación matemática del siglo XVIII.
Espero que sea de su agrado, es importante como la ciencia de la matemática, nos culturiza implementando nueva filosofía del conocimiento, y los avances de las sociedades, para sus desarrollos.
Fuente Bibliográficas.
Algoritmos En C++ - Página 454 por Robert Sedgewick - 1995.
Invitación a la matemática discreta - Página 194 por Jirí Matousek, Jaroslav Nesetril - 2008.
Técnicas gráficas en prodúctica Escrito por Eduardo A. Arbones Malisani pagina 18; - 1992.