Hello steemitonias friends I want to welcome you to the first among a series of three, which refer to the gravitational field of the earth, in each issue will be presented topics of utmost importance and will be touched by stages in depth each delivery, highlighting that this The first installment deals with basic issues of the gravitational field of the earth, basic concepts and mathematical parameters that define it.
The Earth has an approximate mass of 5,974 · 10*kg. This enormous value makes the effects of the gravitational field it generates very evident: you only have to take a leap to realize that the Earth attracts you with great intensity. In this section we will deal precisely with the gravitational field generated by the Earth and some particularities that it presents. We will see:
- The intensity of the field on the earth's surface
- Its variation with altitude and how it is associated with weightlessness
- Its variation with latitude and how it is associated with effective gravity and apparent weight
- How to deduct the value of potential energy in the vicinity of the earth's surface.
Surface intensity on the surface
We define the field strength in the earth's surface as the value that the gravitational field intensity vector takes at any point located on the earth's surface. Its direction and meaning is such that it always points towards the center of the Earth. Its value is usually approximated by:
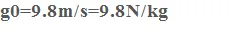
Testing :
To determine the intensity of the gravitational field created by the Earth at any point of its surface, we will consider:
- The Earth as a solid sphere formed by a set of uniform concentric fields. Do not forget, however, that the Earth is actually a little flattened by the poles
- That the average radius of the Earth RT is 6371 km
- That its mass MT is of, approximately 5.974 · 10 kg
These are approximations that will allow us to make calculations that will yield close values very close to the real ones.
We recall that the field strength on the outside of a sphere is given by the expression:
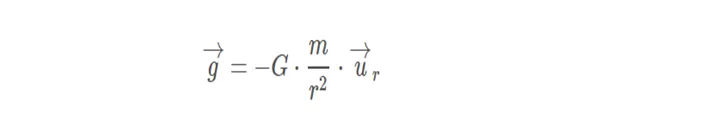
Where G is the universal gravitation constant, m is the mass of the body that generates the field, r is the module of the vector(r) that joins the center of the mass with the point at which we want to determine the field(Ur) and is the unit vector of (r).
Therefore, to determine the value of the field strength on the surface of the Earth, we substitute the indicated values.
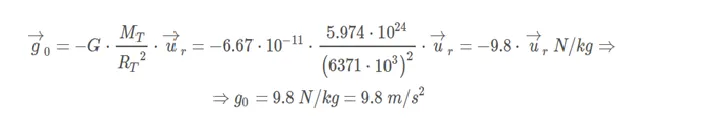
As it can not be otherwise, the direction and sense of the field is always normal to the Earth and pointing towards its center, as they are derived from the multiplication by the unit vector (Ur) and the sign -.
Intensity of the gravitational field on the surface of the Earth
The gravitational field strength vector (g0 ) on the earth's surface is perpendicular to it and pointing towards its center.
The value obtained is an average that varies locally depending on the height, latitude and composition of the subsoil.

Abnormalities on the Earth's surface
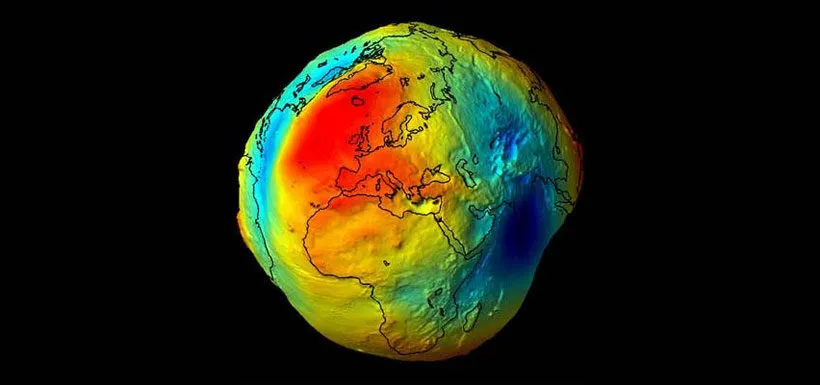
Variations in the composition of the subsoil, such as, for example, mineral or oil deposits, cause local anomalies that affect the value of (g0 ). To measure such anomalies, maps of anomalies such as the figure are usually used. The unit of measurement of these anomalies is usually the milligal (1 mGal = 10-5 N / kg).
Variation with altitude and weightlessness
The intensity of the gravitational field in the vicinity of the Earth varies depending on the height (h) considered on the surface in the form:
Where:
- g , go: Vectors field strength at a generic height on the earth's surface and field strength on the earth's surface respectively. Its unit of measure in the International System (S.I.) is the newton per kilogram (N / kg) that is equivalent to meter per second squared (m / s2) in units of acceleration
- RT: Land radio. Its value is 6371 · 10*3 m approximately. Its unit of measurement in the International System (S.I.) is the subway
- h: Height considered on the earth's surface. Its unit of measurement in the International System (S.I.) is the subway
Testing :
The expression of the field strength is inversely proportional to the distance r to the center of the considered sphere, the Earth in this case. In this way, for a point that is at a height h above the surface, we can write that this point is at a distance r = RT + h from the center of the Earth, leaving the intensity of the field in the form:
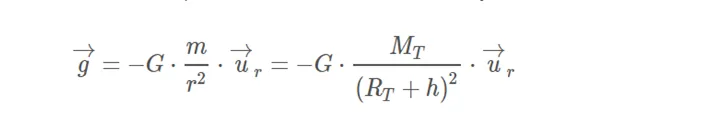
The above expression can be written depending on the field on the surface
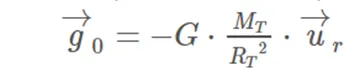 in the way:
in the way:
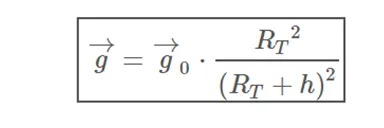

Distance to the center of the Earth
To determine to determine the distance r to the center of the Earth we add to the value of the terrestrial radius RT the height h on the surface.
r = Rt + h
Therefore, as the height h on the surface increases, the field strength decreases, becoming zero at infinity. This contradicts, for example, the supposed weightlessness that astronauts experience in space at heights that are far from infinite. In reality, said weightlessness is the result of a continuous "free fall" that astronauts and ships experience, causing an apparent loss of weight. similar to what you can experience for example when the descent of an elevator begins.

Weightlessness of the astronauts orbiting the Earth
The effect of weightlessness experienced by astronauts and spacecraft that orbit the Earth is mainly due to the apparent weight loss that is the result of continuous free fall that takes place.
Variation with latitude: effective gravity and apparent weight
The intensity of the gravitational field on the Earth's surface varies depending on the latitude α due to the effects of centrifugal acceleration. In the case that we consider a body on the surface of the earth its expression:
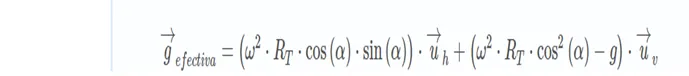
Where:
- (g effective): Effective gravitational field that a body experiences at a certain latitude α. Its unit of measure in the International System (S.I.) is the newton per kilogram (N / kg) that is equivalent to the meter per second squared in units of acceleration (m / s2)
- α: Considered latitude. Its unit of measurement in the International System (S.I.) is the radian (rad)
- RT: It's about the terrestrial radio. Its unit of measurement in the International System (S.I.) is the meter and its value is 6371 · 10*3 m
- ω: Earth's angular velocity. Its unit of measure in the International System (S.I.) is the radian per second (rad / s) and its value 7.2 · 10-5 rad / s
- Uh, Uv: Unitary vectors associated to the intrinsic reference system that has the body on which the calculations are made. They mark the horizontal and vertical senses respectively.
Testing:
The Earth is a body in permanent state of rotation on itself, which makes any other body located on the surface of the same (except if it is located on its axis of rotation) describe a circular motion of radius r. From an intrinsic point of view, that is, from the object itself on Earth, it constitutes a non-inertial reference system and, as such, a centrifugal force will appear on the body that will make the effective value of gravity (g effective) acts on the body vary slightly with respect to what would be if the planet were at rest. The following image illustrates the accelerations to which a body located at point A on the earth's surface is subjected at a latitude determined by α:

Apparent gravity
On the left, the Earth. It is a body in rotation and any other body on its surface located at a certain latitude α experiences the acceleration proper to gravity( g )as well as a centrifugal acceleration (ac). This centrifugal acceleration can be decomposed into a horizontal component (ach) and another vertical (acv).
On the right the effective gravity, fruit of the vectorial sum of the gravity (g) with the centrifugal acceleration (ac).
From the image we can find the following relationships:
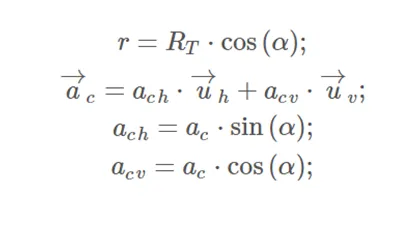
Where we have considered Uh and Uv the unit vectors that define the directions of the horizontal and vertical intrinsic axes respectively. Now, remember that from an intrinsic point of view, and for the case of circular movement, the value or modulus of the centrifugal acceleration and the normal or centripetal acceleration must coincide, being:
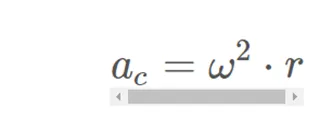
With what we can write:
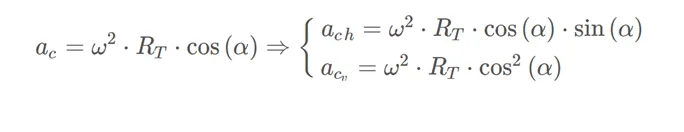
Since g effective = g + ac, if we perform the vector sum we obtain:
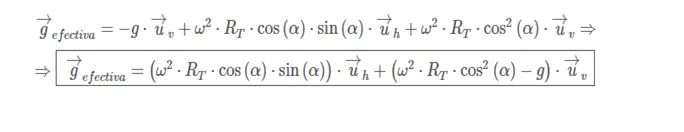
Sometimes the horizontal component is usually neglected, leaving simply
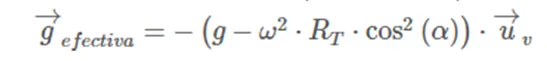
On the other hand, it is direct to calculate the effective or apparent weight associated with effective gravity such as:
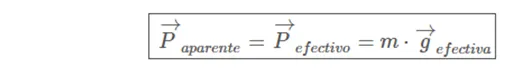
Potential energy in the vicinity of the ground
The potential energy of a body of mass m on the surface of the Earth, of mass M and radius Rt is given by:
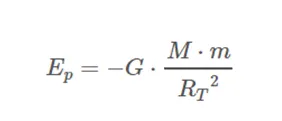
If we place the body at a certain height h above the surface (r = Rt + h), the gravitational potential energy is:
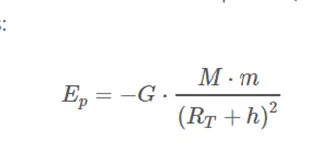
The variation of potential energy between both points:
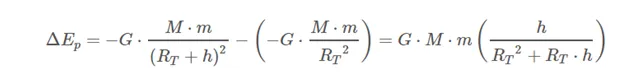
Now, we know that RT >> h, so we can neglect Rt · h versus Rt2. We also know that, on the earth's surface, g0 = G · M / Rt2. With this we can write:
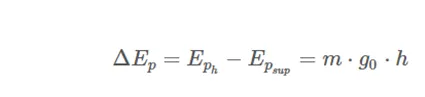
Finally, if we consider the potential energy on the surface 0, Epsup = 0, we obtain the value of the gravitational potential energy in the vicinity of the ground, so used in previous levels:
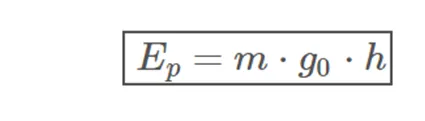
Imagns Source:
https://www.fisicalab.com/apartado/campo-gravitatorio-terrestre#contenidos

