An old, well-known myth claims that holding a seashell up to the ear channels the sound of the ocean.

Conch shells are popular among children for the ocean-swell sound they produce.
While it's true that many shells produce a faint 'whoosing' noise, there's no mystical force at play.
Resonance in cavities is a well-understood, common phenomenon. It's the reason a bottle hums when you blow across the neck and a wine glass vibrates when you rub the rim.
While the sound has absolutely nothing to do with the ocean, it really is caused by waves: sound waves propagating in the surrounding air.
Seashell Sound Chambers
To understand the origin of this swelling noise, we can think of the seashell as a chamber, or pipe. Within the pipe, sound waves oscillate like points on a skipping rope.
Waves of certain wavelengths 'fit' best into the pipe; these waves are often the sum of many other wave frequencies. These waves appear to move only up and down at any given point (in our skipping rope analogy, amplitude is the height of the peak or trough at a point along the rope).
Such a wave can be considered 'stationary' (although the sound vibration itself still propagates, or 'travels') and is termed a standing wave.
Standing Waves
Let's explore standing waves.
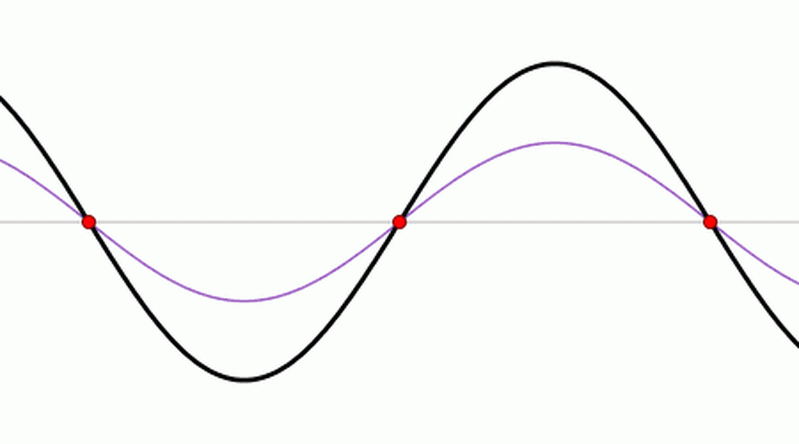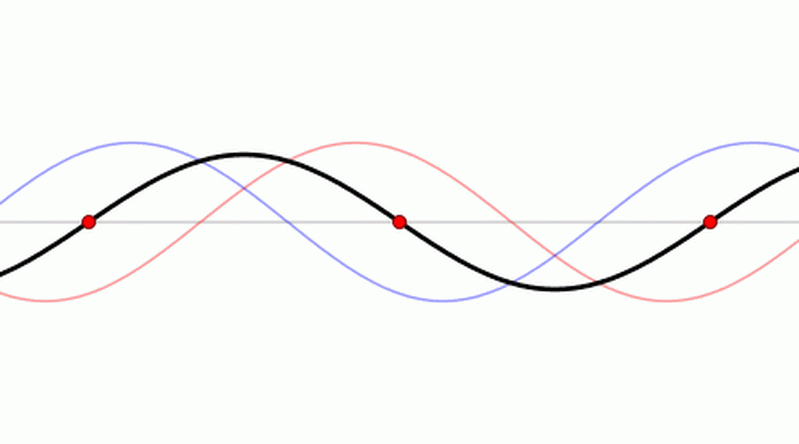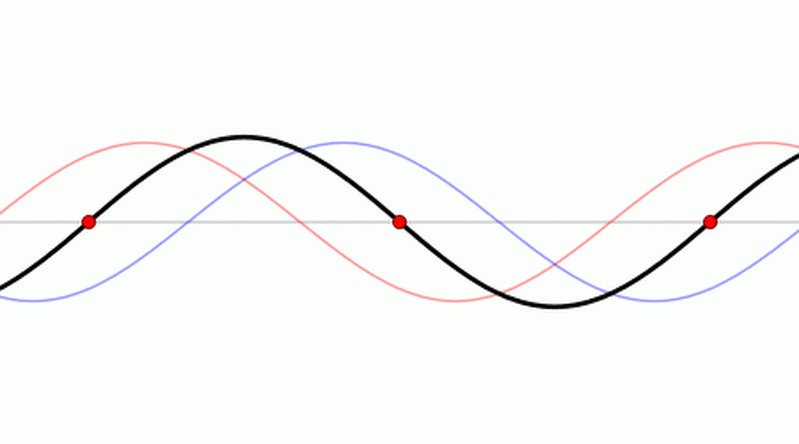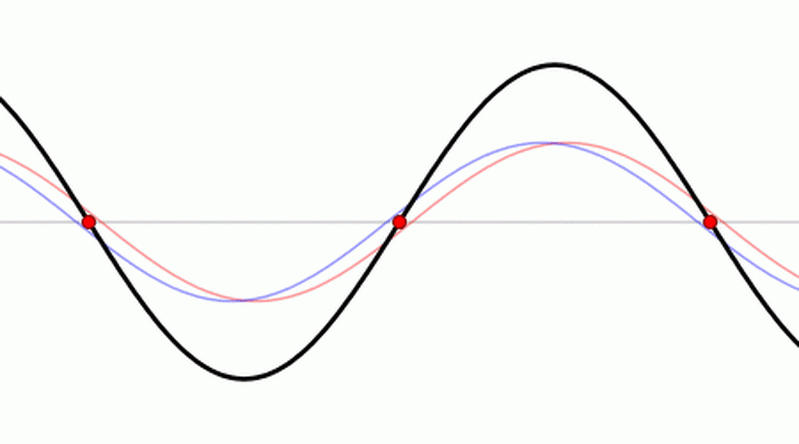
A standing wave in a pipe may only be set up for waves of wavelength such that the amplitude at zero at a wall (at a node) and maximum at an open end (at an antinode).
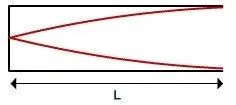
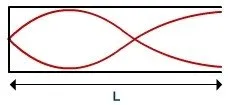
Three-quarters of a wavelength (first overtone) also satisfies these conditions.
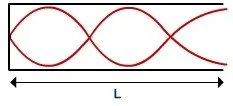
The second overtone, or 5th harmonic, fits five-quarters of a wavelength.
The length of an open-ended pipe must therefore be a quarter of wavelength long (or three-quarters, or five-quarters, or seven-quarter, and so on).
A closed pipe, on the other hand, must feature a node at both ends.
This allows standing waves to be set up in a pipe of length one-half wavelength, one wavelength, three-halves wavelength, and so on.
The scenario for both open and closed pipe standing waves is summarized visually below:

Seashell Resonance
Since only certain wavelengths of sound permit standing waves in a pipe, it follows that only certain pitches of sound set up standing waves ('pitch' being a perceived result of a wave's frequency). These standing waves resonate within the pipe and the result is an amplification in volume - a greater amplitude is equivalent to a greater propagated energy (hence the term 'amplification').
The diagrams above indicate that the resonant sound frequencies will be harmonics (set apart by certain multiples of wavelength fractions).
This explains why the whooshing sound seems layered: the resonating sound comprises many harmonic standing waves.
Seashell Pipe Model
Treating our seashell as a pipe, we come to the conclusion that the sound of the ocean is in fact ambient sounds of certain frequencies resonating as standing waves form within the shell.
The respective pitch of each set of waves is dependent on the size and shape of the shell - some are approximated by an open-ended pipe, while others are best compared to a closed pipe.
Longer shells produce a set of resonant waves of lower frequency, and the set of harmonic sounds (the 'swell of the ocean') has a deeper pitch.
Dispelling The Illusion...
If all this talk of 'standing waves' and 'nodes' seems complicated and disillusioning, don't worry - there's a reason the myth was passed down for generations.
Given the choice between sitting an eight-year-old down by their sandcastle to talk about 'resonant frequencies' or congratulating them on their ocean walkie-talkie, there's only ever one winner.

If you enjoyed this article and want more, follow the everyday science blog for your daily dose of science.
References:
http://indianapublicmedia.org
http://www.physicsclassroom.com