Leonhard Euler (1707-1783 ),source of image of mastery of wikimedia commons.
When we speak of grafos, we allude of Leonhard Euler, mathematician, physicist and Swiss philosopher, it was him who realized big advances in the theory of grafos, the most fascinating thing to be able to come to this theory, the number of Euler (e), as a constant, which the value of the derivative is represented by the slope of the tangent line, of the function f the (x)th = e%x, of such a way when the value of x = 0 this one is equal 1, up to considering natural logarithm or logarithm in base and, having base of support in this logarithm, he developed the theory of grafos or theory of the graphs, basing in the analysis of the properties of the grafos or graphic. Where a grafo is a set, I do not empty of apexes or nodes and a selection of pairs of apexes, which they are edges, considering the following thing, which they can be faced or not, of such a way, which a grafo represents by means of a series of points, in this one cases would be the apexes, at the same time they are connected by lines of the edges.
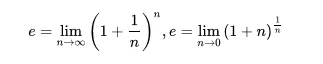
Source of image of mastery of wikimedia commons.
East big contribution served as fundamental base, for the analysis and definition of the logarithmic and exponential functions, after his work of the theory of the grafos, also it discovered the theorem of the composition of integrals elliptical, giving as result him god more perfection to the flat geometry and of solid. It is that's why, that between the simplest and secondhand structures the lists and the counterfoils are, although frequently a combination of both is used in the grafos, since to the theory of grafos it is not interesting to him to know, what sound the apexes, the form of the edges are not excellent, only it imports to what apexes they are joined.

The grafos are the object of study of this branch of the mathematics, the grafo fish, source of image of mastery of wikimedia commons.
But also there exists the case, which if the only edge exists and associated with the tidy pair (v, w) of apexes, we write and = (v, w), which denotes an edge of v to w, to steady itself, that a guided grafo is that one, which has unidirectional unions. It is necessary to take in account the following thing to understand a little more on this content, there exist adjacent apexes, which shape a side or edge, where all the sides shaped by two apexes, it is said that it is incidental on these apexes, if an apex does not have other adjacent says to himself that it is isolated, thanks to it to the moment to chart, the diagrams of the grafos, they can be represented graphicly when the quantity of apexes is not big, because also it allows the case, that two grafos are isomorfos, if mail exists one to one between the nodes of both grafos, and also they preserve the adjacency both between the nodes and in the direction of the sides, by means of the mathematical definite model, G1 = (V1, E1) and G2 = (V2, E2) grafos simple, it are said that G1 and G2 perform isomorfos the same form, if there is a function biyectiva f of V1 to V2, with the property of which to and b, they are adjacent in G1 if and only if f (a) and f (b), they are adjacent in G2, for everything to and b in V1 such a function f, it is called an isomorfismo.
Understand that it is a little complicated, for the technical handling of this mathematical model, but his application is very diverse me reading, such friends as: it served as use of the bend of vertical supports and generated a new branch of engineering with his works on the critical load of the columns, at present it serves us, to design networks, inside the programming for the design of circuits, cartography in the colored one of maps, social sciences, physical sciences, engineering of communication, it is a wide scale of use of this mathematical model characterized by logic of design and graphs.
In the philosophy it had the following position, was insisting that the knowledge bases partly, in the existence of quantitative precise laws, something that the monismo and the philosophical theories of Christian Wolff, were not capable of providing, Since the development of the calculation was one of the principal questions of the mathematical investigation of the XVIIIth century.
Hope that it should be of his taste, it is important as the science of the mathematics, us culturiza implementing new philosophy of the knowledge, and the advances of the societies, for his developments.
Source Bibliographical.
Algorithms In C - Page 454 for Robert Sedgewick - 1995.
Invitation to the discreet mathematics - Page 194 for Jirí Matousek, Jaroslav Nesetril - 2008.
graphic Skills in prodúctica Written by Eduardo A. Arbones Malisani paginates 18; - 1992.