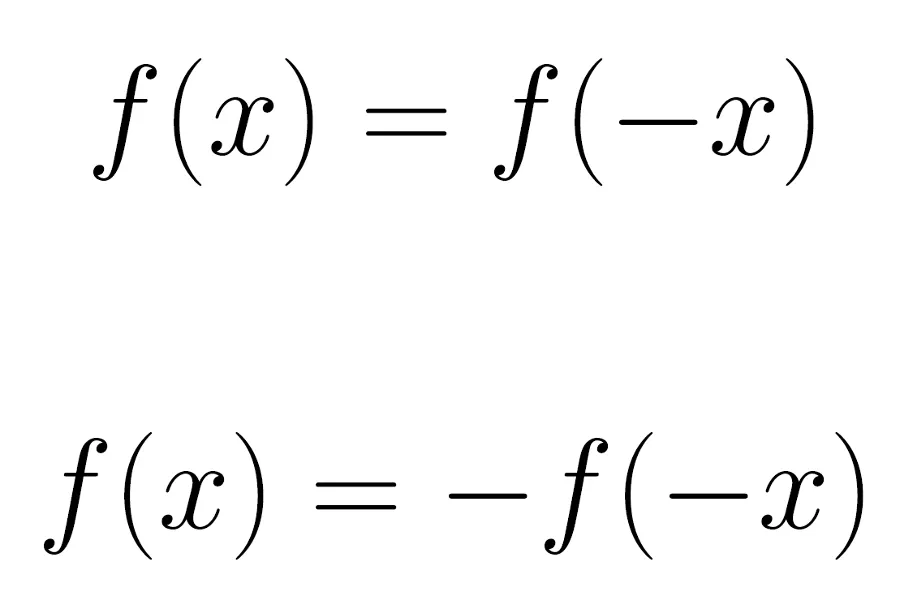
In this post I will discuss the concept of an even function and the concept of an odd function and give some examples of these types of functions. We would like to understand these types of functions because the properties of evenness and oddness allow us to simplify certain calculations such as finding integrals over symmetric intervals on the real line.
An even function is a function f(x) that satisfies f(x) = f(-x) for every value of x in its domain of definition. In words this means that the value of f at the point x and its negative are the same. Geometrically this means that f is symmetric with respect to the y-axis. That is if we have graphed the function f(x) for positive values of x we can determine its graph for negative values of x by reflecting the part we have already draw across the y-axis.
A simple example of an even function is f(x) = x2. To check that this function is even we must show that f(x) = f(-x). This is easily done as follows f(-x) = (-x)2 = x2 = f(x). Another example of an even function is f(x) = cos(x). We can prove this using a trig identity. We have cos(-x) = cos(0 - x) = cos(0)cos(x) + sin(0)sin(x) = cos(x) because cos(0) = 1 and sin(0) = 0.
Now let us consider what happens when we integrate an even function over a symmetric interval, that is an interval of the form [-a, a]. Consider the integral of f(x) = x2 over the interval [-1, 1]. Because our function f(x) is even we can see that the area under f(x) on the interval [-1, 0] is exactly the same as the area under f(x) on the interval [0, 1]. It follows that the integral of f(x) on the interval [-1, 1] is twice the value of the integral of f(x) on the interval [0, 1]. Generalizing this idea to any even function f(x) we see that the integral of f(x) on the interval [-a, a] is twice that of the integral of the same function on the interval [0, a].
An odd function is a function f(x) which satisfies f(x) = -f(-x). A simple example of an odd function is f(x) = x3. This function is odd because we have that -f(-x) = -(-x)3 = x3 = f(x). Another example of an odd function is f(x) = sin(x). We have sin(-x) = sin(0 - x) = sin(0)cos(x) - sin(x)cos(0) = -sin(x) which is equivalent to sin(x) = -sin(-x).
If we integrate an odd function over a symmetric interval [-a, a] then something nice happens. From the graph of an odd function we can see that the integral of an odd function on the interval [-a, 0] is the negative of the integral of the same function over the interval [0, a]. Thus is follows that the integral of an odd function on the interval [-a, a] is always equal to 0. This allows us to calculate integrals of odd functions on symmetric intervals just by looking at the integral.
In this post we have defined the concept of an even function and the concept of an odd function. We have given some simple examples of even and odd functions. Furthermore, we have shown that if we know a function is even or odd this allows us to simplify the calculation of certain integrals.
References:
https://en.wikipedia.org/wiki/Even_and_odd_functions
http://mathworld.wolfram.com/EvenFunction.html
http://mathworld.wolfram.com/OddFunction.html
http://mathworld.wolfram.com/TrigonometricAdditionFormulas.html