안녕하세요. @hkkim1030입니다.
다가오는 태풍시즌에 대비하여,
길고 긴 출장을 마치고 돌아왔습니다.
그동안 너무 포스팅을 못했네요.
미뤄둔 포스팅을 달려볼까 합니다.
[오기 전에 알아두자] 태풍 '노루' 경로 분석하기에서,
@hunhani님으로부터 태풍 경로에 영향을 미치는 인자인
'제트류', '해수면 온도 경도', '몬순 기압골'에 대한 포스팅을 요청 받았습니다.
이것을 설명하기위해,
[아는 것이 힘이다-지구과학#4] 수학으로 바람 이해하기 part1에서
del operator와 divergence/convergence에 대한 개념을 공부했습니다.
오늘 포스팅에서는,
Lagrangian frame과 Eulerian frame에 대한 설명을 해보고자 합니다.
두 가지 frame은 물리적 현상을 풀어낼 때,
추적하며 (lagrangian; x, y, z, t를 모두 고려) 풀어내는가,
혹은, 고정된 상태 (eulerian; t만 고려)로 풀어내는에 따라 다르게 사용되는 풀이 방법입니다.
이 두 가지 프레임을 표현하기 위해서,
전미분 (total differentiation)과 편미분 (partial differentiation) 을 사용합니다.
쉬운 예로
T = T(x,y,z,t)를 정의하고,
taylor seies를 적용하면 아래의 식을 얻을 수 있습니다.

이 식의 의미는 매우 간단합니다.
온도의 총 변화 = x축 이동거리 * x 축만의 온도변화 + y축 이동거리 * y축만의 온도변화 .....
이 식을 시간 변화로 나누면,

다시 풀어쓰면,
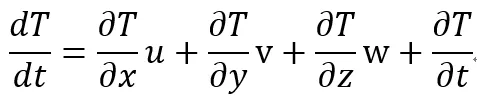
입니다.
위 식에서, u는 x축 바람, v는 y축 바람, w는 z축 바람을 의미합니다.
이 식에 [아는 것이 힘이다-지구과학#4] 수학으로 바람 이해하기 part1에서 배운
del operator를 적용하고 V=V(u,v,w)라 정의하면,

를 얻을 수 있습니다.
위 식에서,
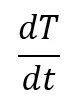 을 Lagrangian frame이라 부르며,
을 Lagrangian frame이라 부르며,
 을 Eulerian frame이라 부릅니다.
을 Eulerian frame이라 부릅니다.
또한, 두 frame을 이어주는
 을 advection (이류) 라고 부릅니다.
을 advection (이류) 라고 부릅니다.
기온을 예측할때, advection은 매우 중요한 요소로 작용합니다.
아래와 같은 그림을 가정해보도록 하겠습니다.

차갑고(cold) 따뜻한(warm) 지역이 있을 때,
 는 차가운 쪽에서 따뜻한 쪽으로 향하게 됩니다.
는 차가운 쪽에서 따뜻한 쪽으로 향하게 됩니다.
이 때, 바람이 오른쪽으로 불면,
 >0가 되며,
>0가 되며,
이를 cold advection이라고 부릅니다.
cold advection이 생기면, 앞으로 이 지역은 온도가 내려갈 것이라고 예측할 수 있습니다.
이번 포스팅은 여기서 마치도록 하겠습니다.
읽어주셔서 감사합니다.
_____________________________________
또한, kr-newbie 태그를 언제까지 사용할 수 있는지 알려주시면 감사하겠습니다.