Sexta Entrega.
En este artículo les presento la resolución en detalle de diez (10) Ecuaciones Diferenciales Ordinarias Lineales de Primer Orden (EDO) Homogéneas, tomadas del libro Ecuaciones Diferenciales. Por: Richard Bronson, Gabriel B. Costa. Tercera Edición. Serie Schaum. Págs. 19, 20, 26, 27, 28 y 30. (Ver referencias bibliográficas). En todos los artículos que hemos entregado y en las próximas entregas a través de esta esta valiosa plataforma de las redes sociales como lo es Hive-blog, las derivadas ordinarias se han escrito usando la notación de Leibniz:
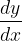
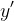, la notación de Leibniz tiene una ventaja sobre la notación prima en que muestra claramente ambas variables, las dependientes y las independientes. Comencemos:
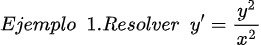
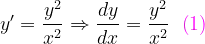
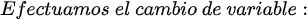
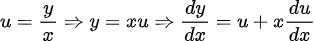
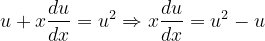
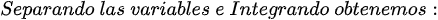
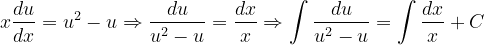
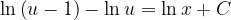
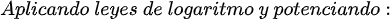
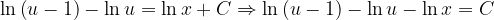
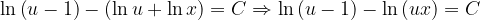
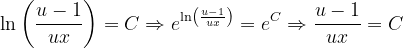
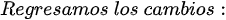
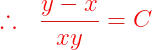
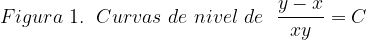
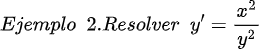
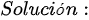
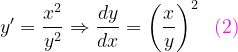
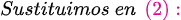
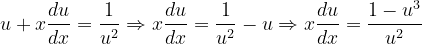
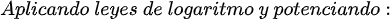
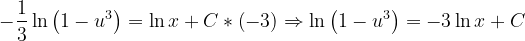
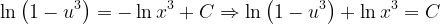
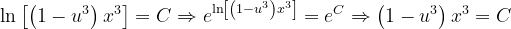
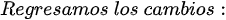
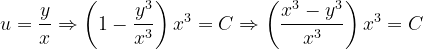
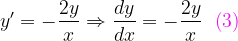
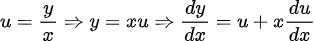
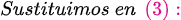
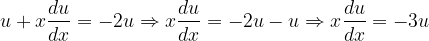
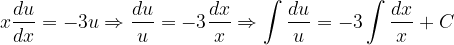
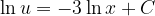
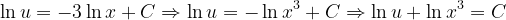
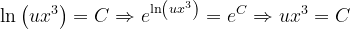
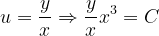
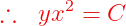
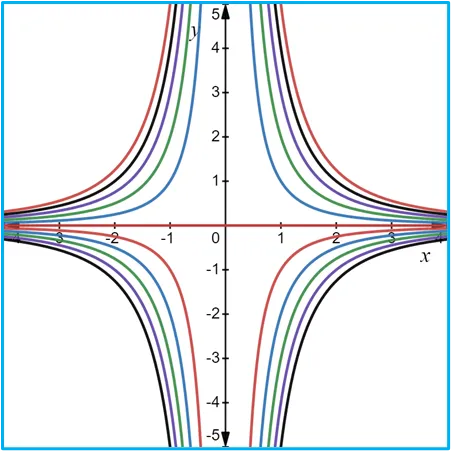
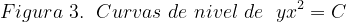
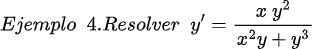
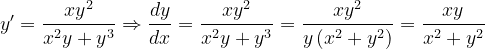
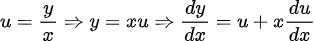
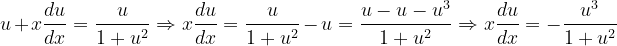
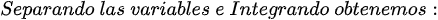
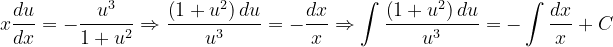
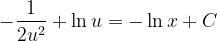
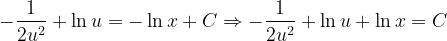
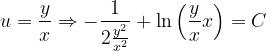
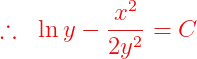
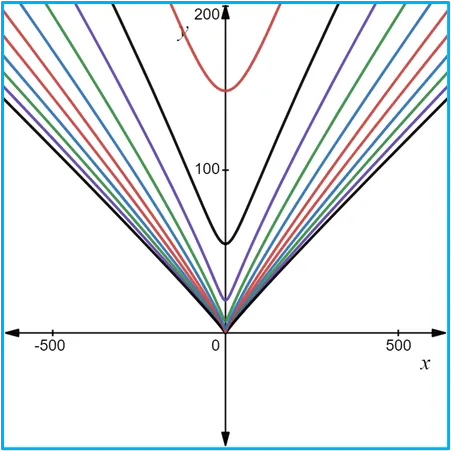
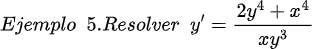
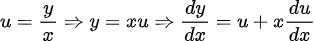
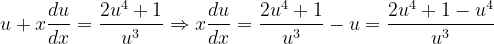
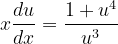
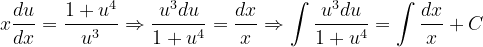
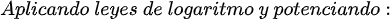
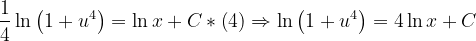
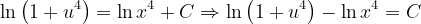
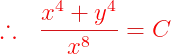
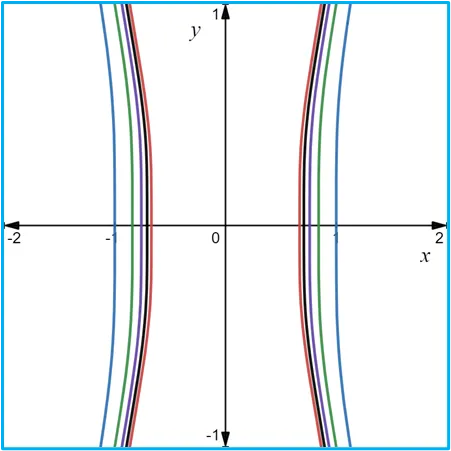
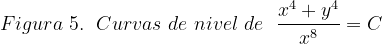
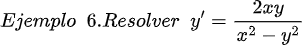
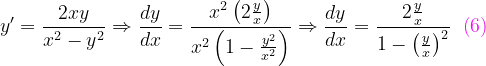
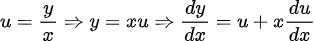
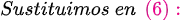
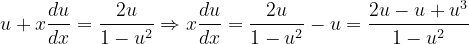
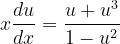
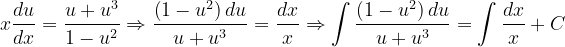
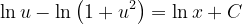
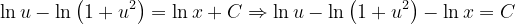
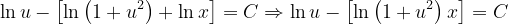
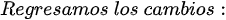
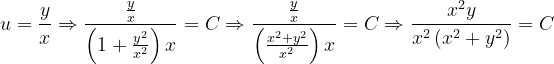
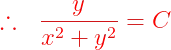
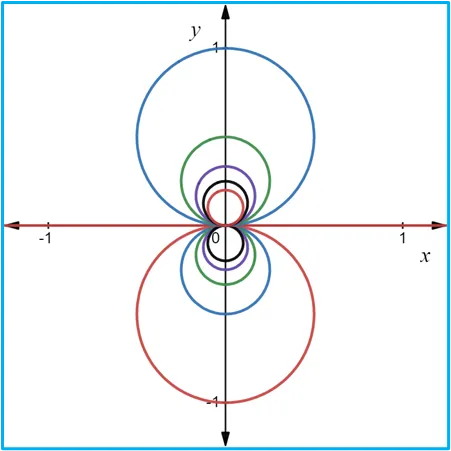
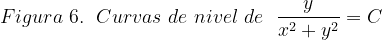
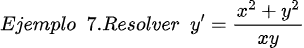
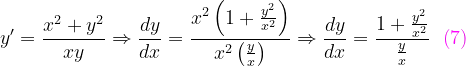
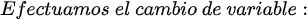
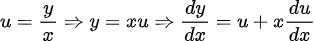
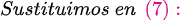
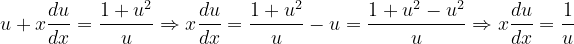
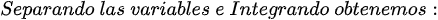
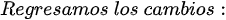
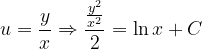
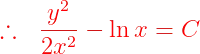
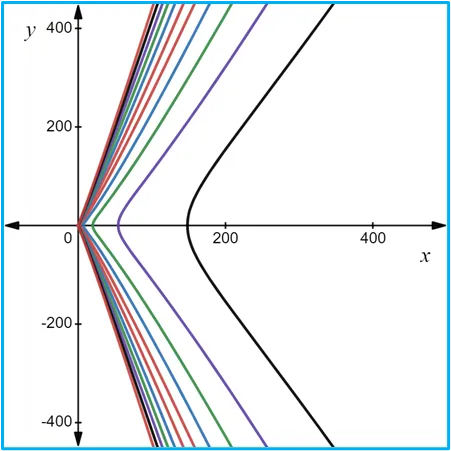
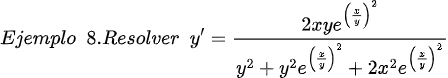
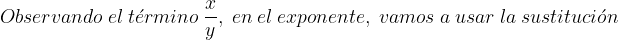
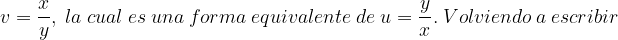
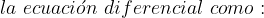
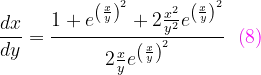
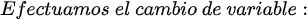
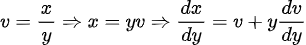
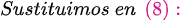
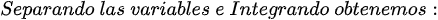
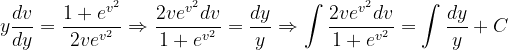
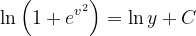
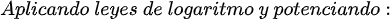
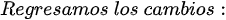
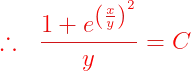
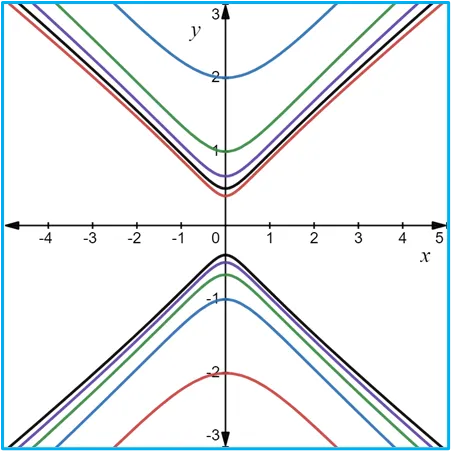
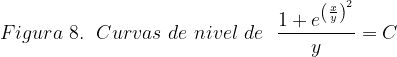
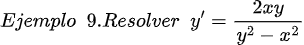
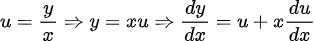
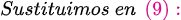
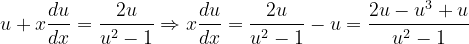
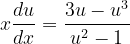
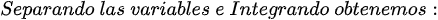
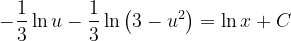
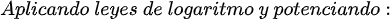
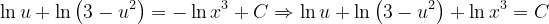
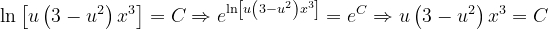
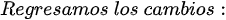
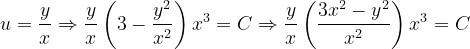
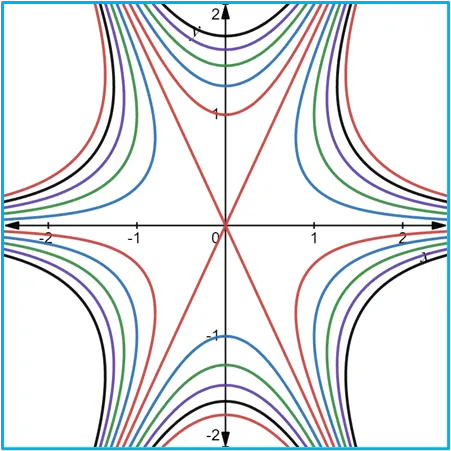
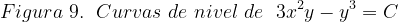
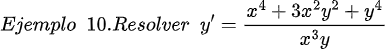
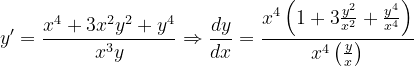
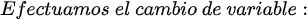
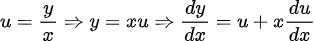
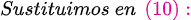
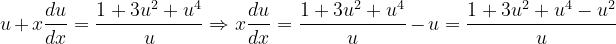
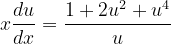
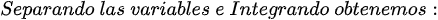
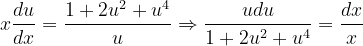
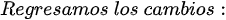
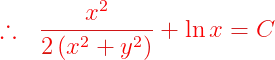
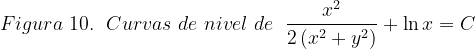
Fuentes bibliográfica.
Nuñez V. Gary L. Solucionario de Ecuaciones Diferenciales de primer Orden, Módulo I: Ecuaciones Diferenciales de Variables Separables. Editorial Latinos, E.E.U.U., 2020.
Dennis G. Zill, Michael R. Cullen. Ecuaciones Diferenciales con problemas con valores en la frontera. Séptima Edición. México: Cengage Learning Editores, 2009.
R. Kent Nagle, Edward B. Saff, Arthur David Snider. Ecuaciones Diferenciales y problemas con valores en la frontera. Séptima Edición. México: Pearson Educación, 2005.
Richard Bronson, Gabriel B. Costa. Ecuaciones Diferenciales. Tercera Edición. Serie Schaum. Editorial Mc Graw Hill.
Fuente de las imágenes.
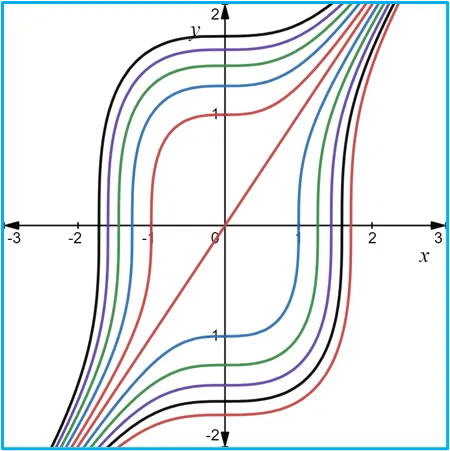
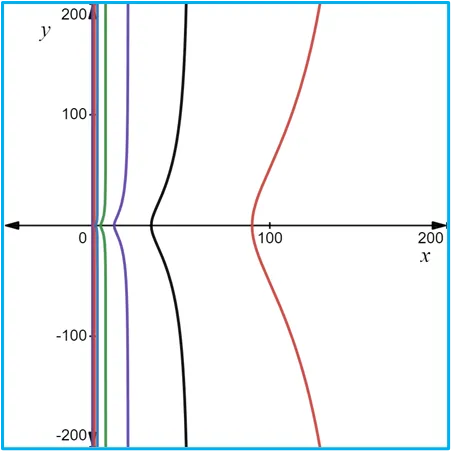
Las gráficas de las curvas de nivel se construyeron usando la página web: https://www.desmos.com/calculator/frx7bimvdd?lang=es.