Mathematics - All About Trigonometry (Part 3)

Introduction

Hey it's a me again @drifter1!

Today we continue with the small series about Trigonometry. I suggest reading the first and second parts before getting into this one. Today we will cover how we solve non-right-angled Triangles

So, without further ado, let's get straight into it!

Solving Non-Right Triangles

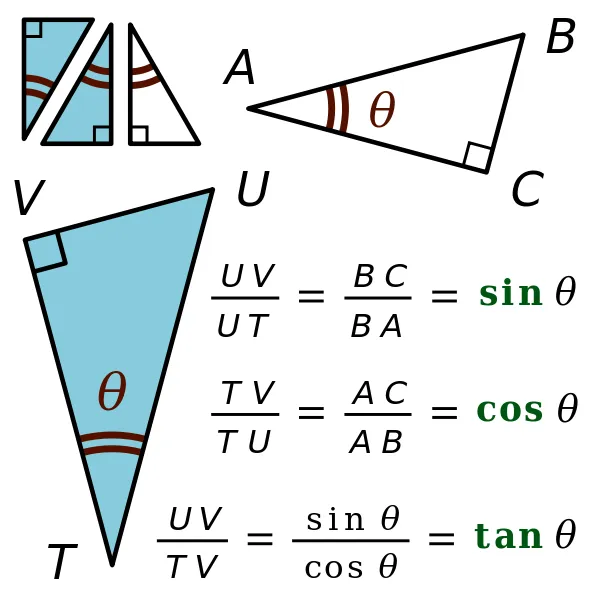
When speaking of Right Triangles, because an angle is already known (the right angle of 90°), only two more values are needed, which can be either angles or sides, in order to solve the whole triangle. More specifically, the solution can be found using Pythagoras's Theorem and the basic trigonometric functions (sin, cos, tan) quite easily.

But, what about non-right triangles, or any general triangle, so to speak?

In general, to solve a triangle, you need to know:

Three Angles (AAA) → Only calculate the ratio of the sides (can't find the actual size of the triangle)
Two Angles and a Side not between them (AAS)
Two Angles and a Side between them (ASA)
Two Sides and an Angle between them (SAS)
Two Sides and an Angle not between them (SSA)
Three Sides (SSS)

Before getting into how each of these cases is solved, its necessary to cover specific Trigonometric Laws...

Law of Sines (or Sine Rule)

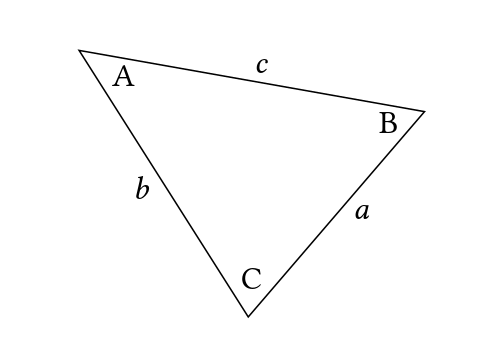
Let's consider the following general triangle:

[Image 2]

The Law of Sines states that:

if a, b and c are sides of a triangle, and
if A, B and C are angles of a triangle, and
side a is facing angle A, side b is facing angle B and side c is facing angle C, then
dividing side a by the sine of angle A is equal to side b divided by sine of angle B and also equal to side c divided by the sine of angle C

Mathematically:

It's also common to turn the fractions upside-down:

Usefulness

The Law of Sines can be used to:

Calculate an unknown angle, when two sides and one angle are known
Calculate a unknown side, when one side and two angles are known

Of course, in both cases, the angles and sides have to be facing each other in order for the Fractions to work.

For example, knowing angle A and sides a and b, we can calculate angle B. Similarly, knowing the angles B and C, and the side c, we can calculate side b.

Sometimes Two Solutions

In the case of SSA problems (two sides with the angle not between them), the remaining angle can give:

a smaller triangle (acute triangle - all angles less then 90°), or
a wider triangle (obtuse triangle - has an angle with more than 90°)

Both solutions are equally right and related (mentioned last time):

Law of Cosines (or Cosine Rule)

The Law of Cosines is a extended version of Pythagoras's Theorem.

Solving for side c in a general triangle, the term of -2abcos(C) has to be added on the left side, or mathematically:

The cosine of an angle of 90° or π/2 radians is 0, which explains why Pythagoras's Theorem works on Right-Angled Triangles.

Usefulness

The Law of Cosines can be used to:

Calculate a unknown side, when two sides and the angle between them are known (case SAS)
Calculate the angles of an triangle, when all three sides are known (case SSS)

To calculate the sides use one of the folowing:

It's easy to just remember the c^2 = ... case and switch out the letters!

To calculate the angles use one of the following:

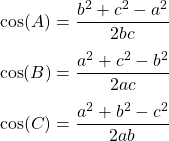
Similarly, one can either solve for cos(X) = ... from the correct x^2 = ... form, or remember the cos(C) = ... case

Remember that the cosine is positive in Quadrant A and negative in Quadrant B, which means that there are no equal values, and so only one solution comes out of the Cosine Rule.

Triangle Cases

So, now that the Laws are out of the way, let's get into each of the previously mentioned triangle cases!

AAA Triangles

AAA triangles (all angles known) are basically impossible to solve. Using Trigonometry its only possible to find the shape, but not the actual size. The length of at least one side is necessary in order to continue...

AAS and ASA Triangles

AAS and ASA triangles (two angles and one side which is between or not between the angles) are solved as follows:

Find the remaining angle, using the rule: sum of all interior angles always adds up to 180° or π radians
Apply the Law of Sines to find each of the other two sides

SAS Triangles

SAS triangles (two sides and the angle between them) are solved as follows:

Apply the Law of Cosines to find the unknown side
Apply the Law of Sines to find the smaller of the two angles (angle facing the smallest side - very important when dealing with obtuse triangles!)
Find the remaining angle, using the rule: sum of all interior angles always adds up to 180° or π radians

SSA Triangles

SSA triangles (two sides and an angle not between them) are solved as follows:

Apply the Law of Sines to calculate one of the other two angles
Find the remaining angle, using the rule: sum of all interior angles always adds up to 180° or π radians
Apply the Law of Sines, once again, to calculate the unknown side

SSS Triangles

SSS triangles (all sides known) are solved as follows:

Apply the Law of Cosines, twice, in order to calculate two of the angles
Find the remaining angle, using the rule: sum of all interior angles always adds up to 180° or π radians

Full-on Examples

Let's skip AAA triangles and get into examples of each of the other types!

AAS Triangle (same process for ASA)

Let's consider the following triangle, with two angles and one side (not between the angles) known: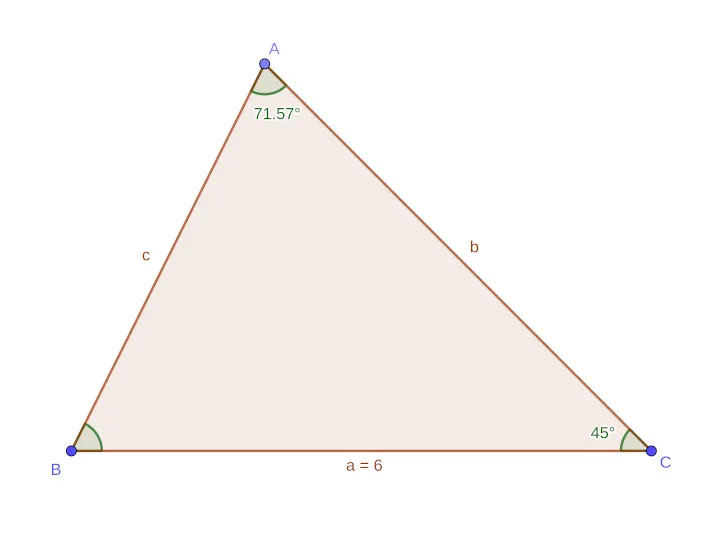

[Custom Figure using GeoGebra]

Because two angles are known, using the rule of 180°, the remaining angle B is easily calculated to be:

Applying the Law of Sines, knowing side a, and angles A and B, its easy to calculate side b:

Applying the Law of Sines, again, its now also possible to calculate side c, using either side/angle pair:

All the sides and angles have now been calculated. Triangle solved!

SAS Triangle

Let's consider the following triangle, with two sides and the angle between them known: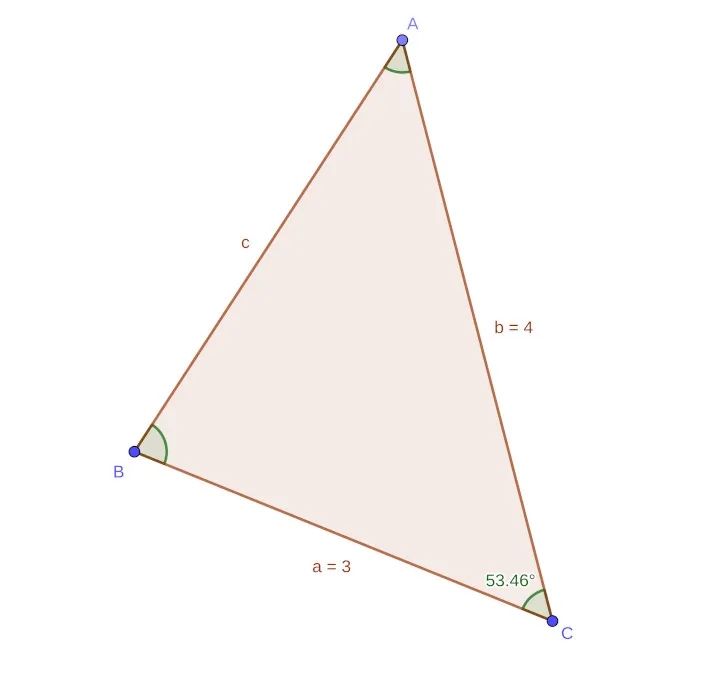

[Custom Figure using GeoGebra]

Because two sides are known, as well as the angle between them, using the Law of Cosines, its easy to calculate the remaining side c:

Next apply the Law of Sines for the smaller of the two angles, which in this case is a, and thus calculate angle A:

Lastly, from the 180° rule, the remaining angle B is:

SSA Triangle

Let's consider the following triangle, with two sides and an angle known, which is not between: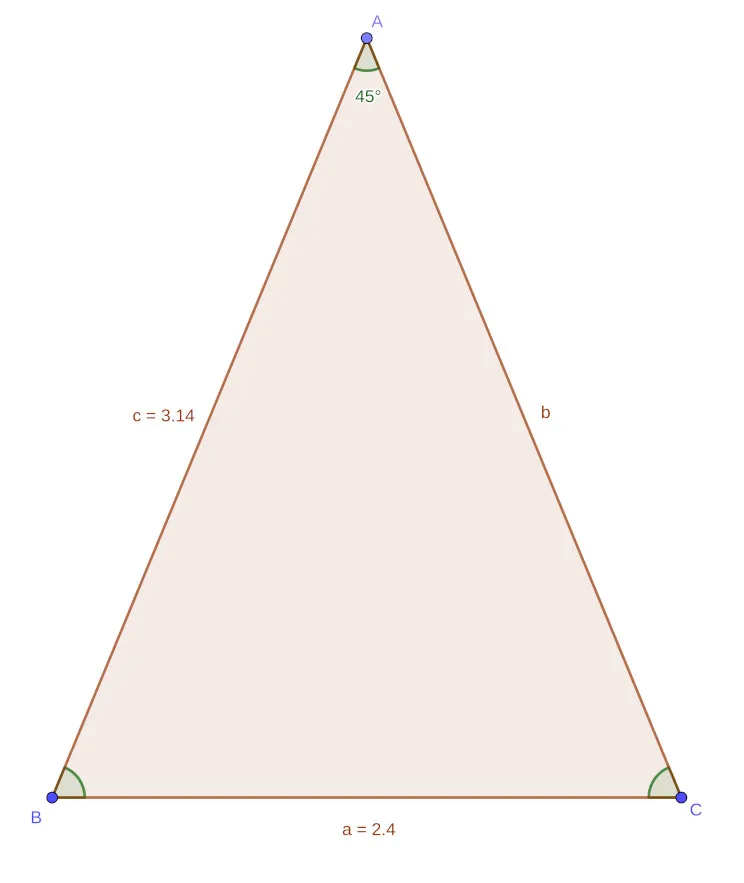

[Custom Figure using GeoGebra]

Two sides are known, but not the angle between them, which means that the Law of Cosines doesn't work in this case. Thus, it's necessary to apply the Law of Sines in order to calculate one of the other angles.

Because sides a and c, as well as the angle A are known, using The Law of Sines angle C is calculated to be:

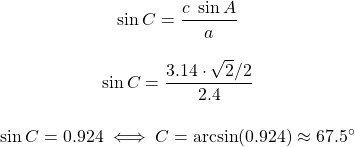
The remaining angle B can be calculated using the rule of 180°, giving:

Applying the Law of Sinues once more, side b can also be calculated:

And so the triangle is Isosceles!

SSS Triangle

Let's lastly consider the following triangle, with all three sides known:

[Custom Figure using GeoGebra]

In this case, only the Law of Cosines works. The Law is applied twice in order to get two of the angles. The last angle can be calculated using the rule of 180°.

Let's first calculate angle C:

Let's next calculate angle A:

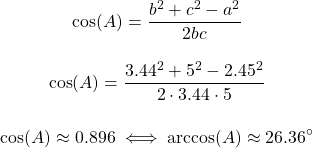
Using the rule of 180°, angle B is:

And this is it! The last triangle has been solved!

RESOURCES:

References

Images

Mathematical equations used in this article, where made using quicklatex.

Final words | Next up

And this is actually it for today's post!

Next time we will get into Trigonometric equations and identities etc.

Also, currently my ideas for "All About" articles include:

Geometry
Polynomial Arithmetic
Exponentials and Logarithms
Rational Expressions

Basically High-School Math Refreshers for Students in Universities or maybe even Middle-Age people that have problems helping their kids out in Math at school!

See ya!

Keep on drifting!