
Let's talk about hashing functions, and specifically about how SHA-256, the hashing algorithm used in bitcoin, works.
The name SHA stands for secure hashing algorithm, and SHA-256 was developed by the NSA and first published in 2001. It is based on the Merkle-Damgaard construction. The intention of this algorithm is to create a secure one-way compression of input data into a fixed-length output. This output also has to be collision-resistant, i.e. it is very hard to find two different input data that produces the same output.
SHA-256 outputs are 256 bits long, hence the name.
One important aspect of hashing functions used in cryptography is that they are 'pseudo'-random, which means that the output of the function looks random, but it is always the same for a given input.
Now, if this is not a sufficient explanation of the algorithm, you can see a more thorough description below. But be warned, it gets a little technical.
SHA-256
Let's begin by outlining some constants, operations and functions. Then we will be well equipped to understand the algorithm.
Specifically we will need to do the following:
- Define constants and hash values
- Define operations
- Define functions
- Run the algorithm
Constants and hash values:
Before we can begin hashing we need to define a starting state and some constants. Specifically, we need eight hash values and 64 constants.
Firstly, we'll Initialize the eight hash values by taking the fraction of the square root of the first 8 prime numbers, in binary form.
We label these a to h.

We will now create 64 constants in the same way as we created the hash values, except this time it's the cube root of the first 64 prime numbers. We label these k0 to k63.
Operations:
Here we will define the five main operations of the hashing algorithm. These will be used in the functions described below.
Right-shift (X, input) :
This operation moves bits in an input right by the specified amount. Note that the rightmost 1 has moved outside the binary number and is now lost. If you were to reverse engineer this operation you would have no way of knowing if that digit was a 1 or a 0.
Right-shift (1, 01100011) => 00110001
Right rotation (X, input) :
Bits are rotated to the right. Note that the rightmost 1 has moved to the leftmost place.
Right rotation (1, 01100011) => 10110001
XOR:
XOR is a logic operation, where you take a number of inputs and output a 1 if one of the inputs is one, but not both. Again, if you try to reverse engineer this you cannot be certain which combination led to the output.
Choice (word1, word2 word3):
This operation takes three inputs. It uses the input of the first word to determine if to take second or third. If it's a 1 it takes the number from the second word, otherwise from the third.
Word 1 = 01100001
Word 2 = 10011000
Word 3 = 11011111
Output = 10011110
Majority (word1, word2, word3):
Takes the majority of the bits of the three words.
Word 1 = 01100001
Word 2 = 10011000
Word 3 = 11011111
Output = 11011001
Functions:
These functions essentially toss the data around and use XOR operations to make it very hard to reverse the algorithm. Each function takes one input, creates three new variables based on right rotation or shifting of the initial variable, and then XOR those variables.
This creates an efficient one-way compression, i.e. you can get a hash from an input but it's very hard to retrieve input from a hash.
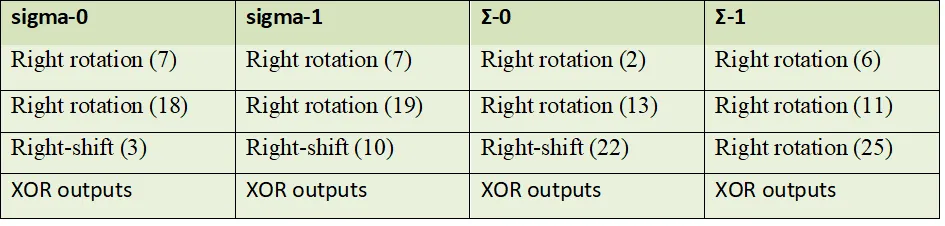
Algorithm:
Finally, having defined the constants, operations, and functions, let's hash the word 'Secret'.
We will do this in three steps:
- Format input data
- Create a message schedule
- Compress the data
1 - Format input data:
We first get the bit representations of the ASCII versions of each letter.
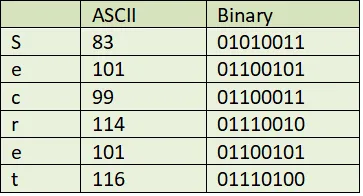
Combining these binary values we get our starting code:
01010011 01100101 01100011 01110010 01100101 01110100
This code is only 48 bits long. However, the SHA-256 needs a 512-bit word. So we need to pad it with zeros. To do this first we add a 1 as a divider, and then we add the zeros. Now we need to reserve the final 64 bits of the word for the message length, which we know is 48 bits. In binary 48 = 110000.
2 - Create a message schedule:
We now want to split our input data into 512-bit chunks, and since this is a short message, we only have one. This is then further divided into 32 bit "words".
Here is our input data for "Secret"
01010011011001010110001101110010 01100101011101001000000000000000
00000000000000000000000000000000 00000000000000000000000000000000
00000000000000000000000000000000 00000000000000000000000000000000
00000000000000000000000000000000 00000000000000000000000000000000
00000000000000000000000000000000 00000000000000000000000000000000
00000000000000000000000000000000 00000000000000000000000000000000
00000000000000000000000000000000 00000000000000000000000000000000
00000000000000000000000000000000 00000000000000000000000000110000
As you can see, we've only got 16 words, and we will need 64 in total. Each following word will depend on specific prior words with the following formula:
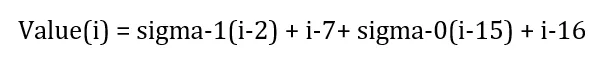
Below you can see a representation of what this formula does. For each new value, we take the inputs relative to the position of that value. This is done until we have 64 words.
Words
1 01010011011001010110001101110010
2 01100101011101000000000000000000
3 00000000000000000000000000000000
...
15 00000000000000000000000000000000
16 00000000000000000000000000110000
17 = sigma1(15) + 7 + sigma0(2) + 1
18 = sigma1(16) + 8 + sigma0(3) + 2
18 = sigma1(17) + 9 + sigma0(4) + 3
And so on..
3 - Compress the data:
We now need to create two temporary words, T1 and T2, using the following formulas:

Remember that word 1 is the first word in the list above and a-h are the hash-values we defined earlier. k0 is the first constant we defined earlier. These temporary words are generated for each word in your list, and the k constant incremented by 1 for each time. After creating the constants, create an initial state with the variables a-h as shown in the table below.
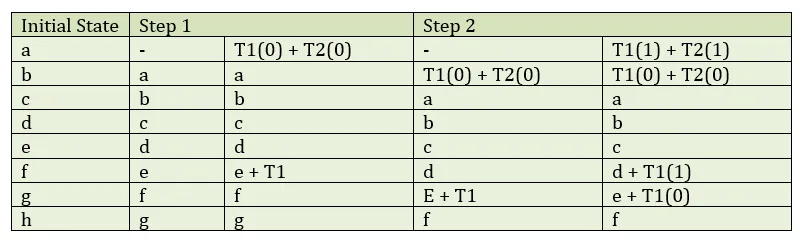
Now, move all words in state register down once. This empties register a and dumps the last one (h). Then add T1+T2 to a and add T1 to e.
Do this for all 64 words, generating new temporary words each time. Finally, add the original a-h to the new a-h.
If this is the last message chunk, convert a-h to hexadecimal and you have your hash: 7e32a729b1226ed1270f282a8c63054d09b26bc9ec53ea69771ce38158dfade8
Closing thoughts
What you end up with is called a digest, and it is the output of the SHA-256 algorithm. This is a fast and secure way to create a digital fingerprint of any type of data and is used for authentication and proof of work in the bitcoin blockchain.
Well done for coming this far!
If you have suggestions or want to add something, please leave a comment below!