
[Image 1]
Introduction
Hey it's a me again @drifter1!
Today we continue with Mathematics, and more specifically the branch of "Discrete Mathematics", in order to get into Set Operations.
I highly suggest checking out the previous part before this one...
So, without further ado, let's get straight into it!
Venn Diagrams
Venn diagrams are illustrations which use circles for the purpose of representing the relationship between various things. If the things have common elements the circles will overlap.

Such diagrams are commonly used in set theory and logic theory to represent the relationship between sets and data, or the operations visually.
Set Operations
Using Venn Diagrams, let's explain the basic operations on sets.
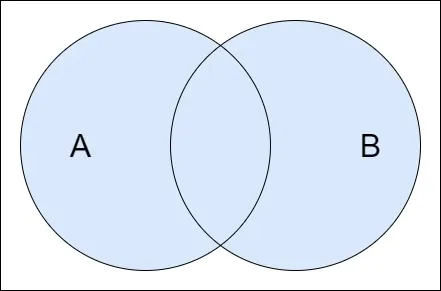
Union
The union of sets A and B, denoted by A ∪ B, is a set which contains elements that belong to A or B or both. Visually:
Intersection
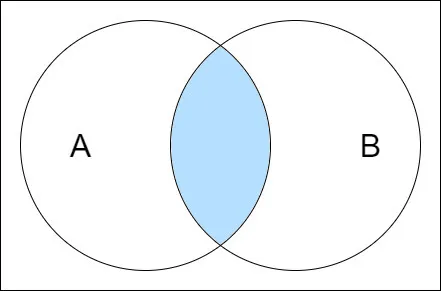
The intersection of sets A and B, denoted by A ∩ B, is a set which contains elements that belong to both A and B. Visually:
Difference
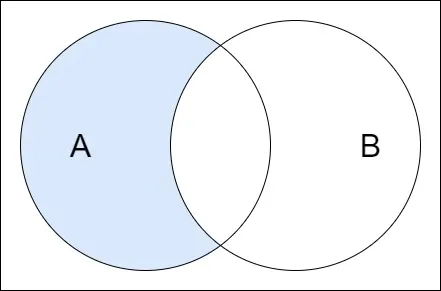
The difference of sets A and B, denoted by A - B, is a set which contains elements that belong to A but do not belong to B. Visually:
Complement
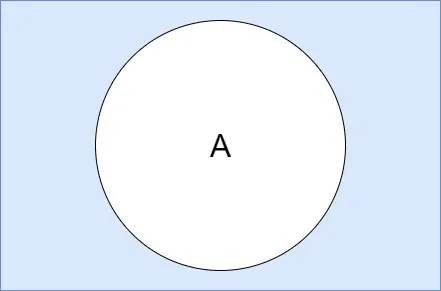
The complement of a set A is a set of all elements that do not belong to A. It's denoted in multiple ways, such as A', Ā, AC etc. Visually:
Symmetric Difference
The symmetric difference of sets A and B, denoted by A ⨁ B, is a set which contains elements that belong to A or B but not both. Visually:

Properties of Set Operations
The set operations mentioned satisfy many properties or Laws of Algebra, which are quite useful and listed in the table below.
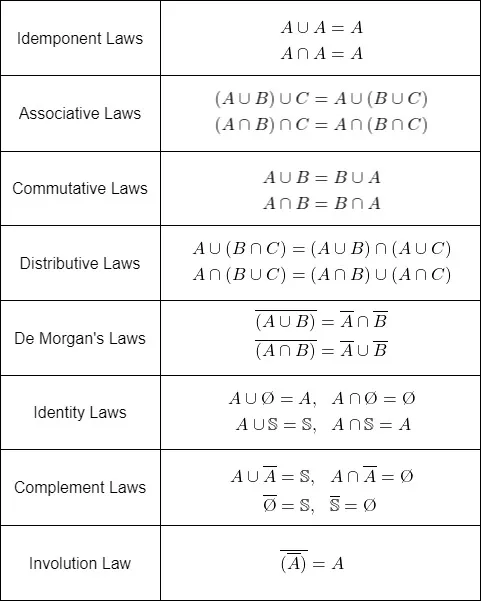
In this table the calligraphic S denotes the universal set of all elements. Other commonly used symbols are V and U. Of course, this doesn't define what exactly "everything" is. If the only concern are natural numbers, then using N would make it easier to comprehend the valid numbers. Similarly, if the numbers of the sets are only integers, the integer set Z would be used instead.
Exercise
Consider the following Venn diagram.
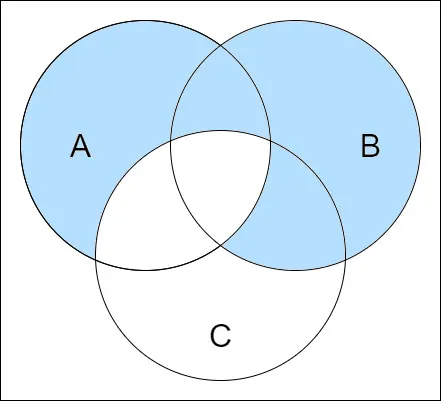
Write an equation for the marked region.
RESOURCES:
References
- https://www.javatpoint.com/discrete-mathematics-tutorial
- http://discrete.openmathbooks.org/dmoi3.html
- https://brilliant.org/wiki/discrete-mathematics/
Images
Mathematical equations used in this article, have been generated using quicklatex.
Block diagrams and other visualizations were made using draw.io.
Previous articles of the series
- Introduction → Discrete Mathematics, Why Discrete Math, Series Outline
- Sets → Set Theory, Sets (Representation, Common Notations, Cardinality, Types)
Final words | Next up
And this is actually it for today's post!
Next time we will continue on with more on Sets...
See ya!

Keep on drifting!
