Buying and Selling Game Contest 16 Results

What is the Buying and Selling Game?

For the benefit of those who have not entered this contest, here is a brief explanation of how the game works.

Participants are required to buy goods with an allocated amount of money. They are given a choice of 6 goods and all these goods are available in any of the 5 towns, cities, islands or planets in the game. The buying prices of all goods are provided in the question.

The participants are then required to sell all of their goods on a future date. The selling prices for all goods in all towns, cities, islands or planets are not provided. Instead, the question provides a triangle distribution for the selling price of each good in each town, city, island or planet. For the triangle distribution, the minimum, maximum, and mode values are provided.

The participant that has the most money after selling all his or her goods is the winner.

Responses to the contest are made in the comments section of the post. If several participants make the same amount of money, the person who entered (commented) first will win. The format of the required entry is explained in detail in the contest itself.

For a more detailed explanation, you can access the contest post using the following link.

Results of the contest

Table 1 contains the selling prices generated by the ‘Buying and Selling’ Game model for each office stationary item from each town or city.

Table 1: Selling prices of all office stationary items for each town and city

Table 2 contains responses and the profit made by each participant.

Table 2: Participant responses and profit

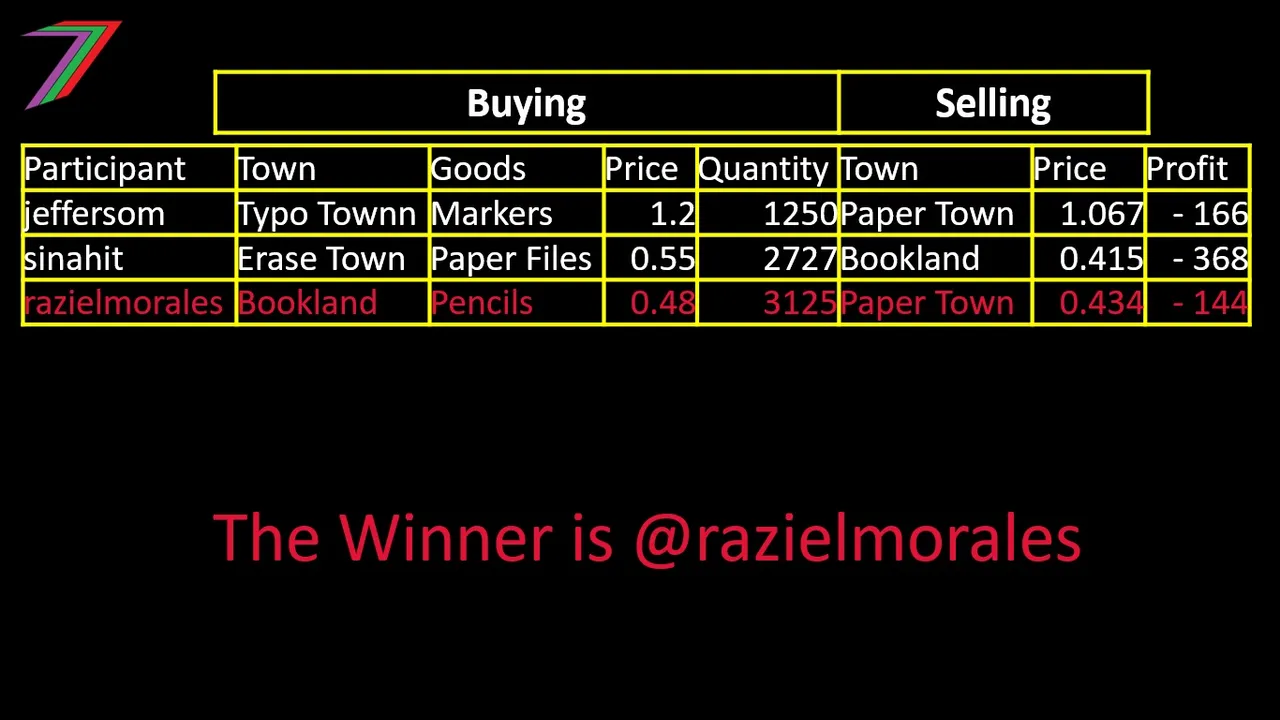
Congratulations to @razielmorales for winning Contest 16 of the 'Buying and Selling’ Game and a prize of 30 Hive.

In Bookland, she bought 3125 pencils at $0.48 each. She paid a total of $1,500.

In Paper Town, she sold the 3125 pencils at $0.434 each. She received a total of $1,356. Therefore, she made a loss of $144 (1,500 – 1,356) or a negative profit of -$144. @razielmorales is our first ever winner to make a loss.

Highest possible profit

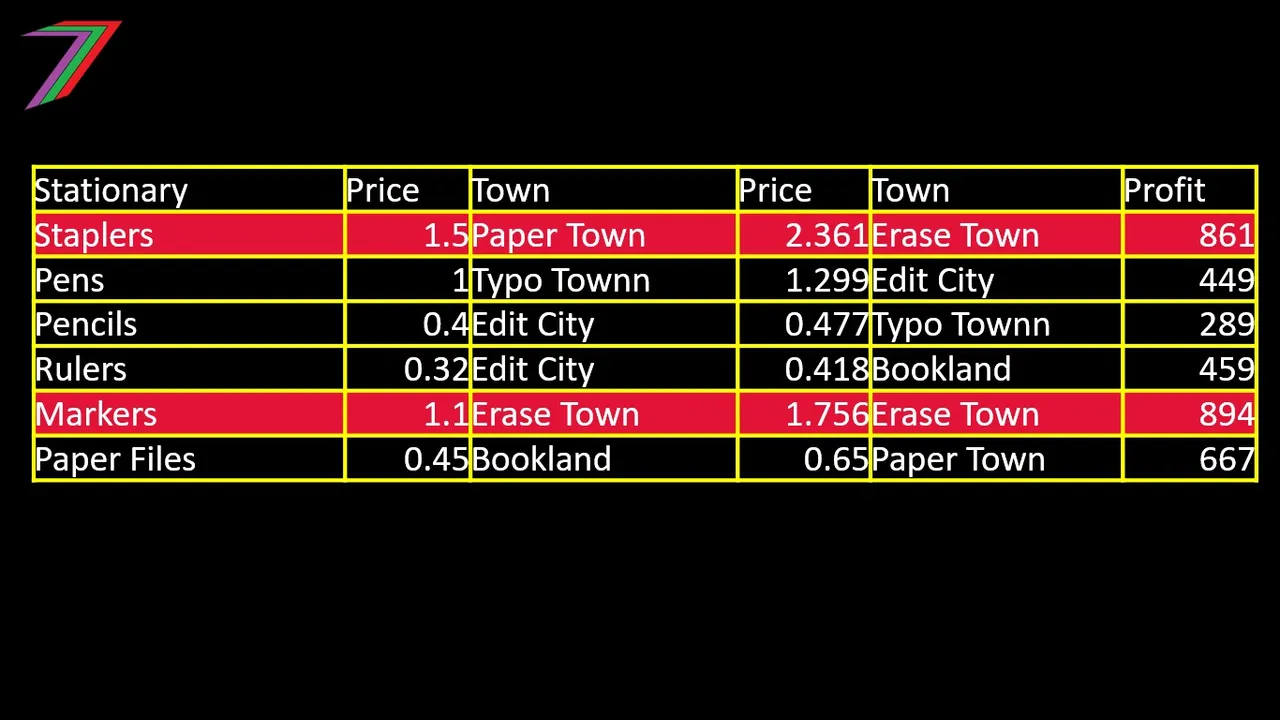
The strategy that would have generated the highest profit would have been to buy 1363 markers from Erase Town at $1.1 each and then selling them at Erase Town for $1.756 (as generated by the model). This would have generated a profit of $894.

This is the first time, for this contest, that buying and selling a good in the same town generated the highest profit. For markers, Erase Town had a minimum price of $0.44 and a maximum price of $2.20. The model generated a price closer to the maximum price than the minimum price. It is possible that the model could have generated a price lower than $1.10, which would have resulted in a loss from selling the markers in Erase Town.

Another good strategy to adopt would have been to buy 1,000 staplers in Paper Town and then sell them in Erase Town. The median price for staplers in Erase Town was $1.86, which is 24% ($0.36) higher than the $1.50 buying price in Paper Town. If this strategy had been used, a profit of $861 would have been made. The model generated a price of $2.361 in Erase Town (higher than both the median selling price and buying price).

Table 3 contains the lowest buying prices, the highest selling prices and the highest profit for selling each office stationary item.

Table 3: Lowest buying price and highest selling price

I would also like to thank @sinahit, and @jeffersom for participating.

Tips for future games (If you want to participate in the next contest, I strongly recommend you read this section of the post)

To achieve the best chance of winning the game (i.e. earning the highest profit). Participants need to make the best use of the information they are given. The participant should buy from the place that sells the good at the lowest price and sell at the place that will offer the highest price.

To inform the decision further, participants should also consider the mean and median prices for each good in each place. The mean and median for a triangle distribution can be calculated using the following formulae.

Mean = (Minimum + Maximum + Mode)/3

Median when Mode ≥ (maximum – minimum)/2 (i.e. mode closer to maximum)
Minimum + (((maximum – minimum) × (mode – minimum))/2)^0.5

Median when Mode ≤ (maximum – minimum)/2 (i.e. mode closer to minimum)
Maximum - (((maximum – minimum) × (maximum – mode))/2)^0.5

Proof Median

More posts

If you want to read any of my other posts, you can click on the links below. These links will lead you to posts containing my collection of works. These 'Collection of Works' posts have been updated to contain links to the Hive versions of my posts.

My New CBA Udemy Course

The course contains over 10 hours of video, over 60 downloadable resources, over 40 multiple-choice questions, 2 sample case studies, 1 practice CBA, life time access and a certificate on completion. The course is priced at the Tier 1 price of £20. I believe it is frequently available at half-price.

Future of Social Media

▶️ 3Speak