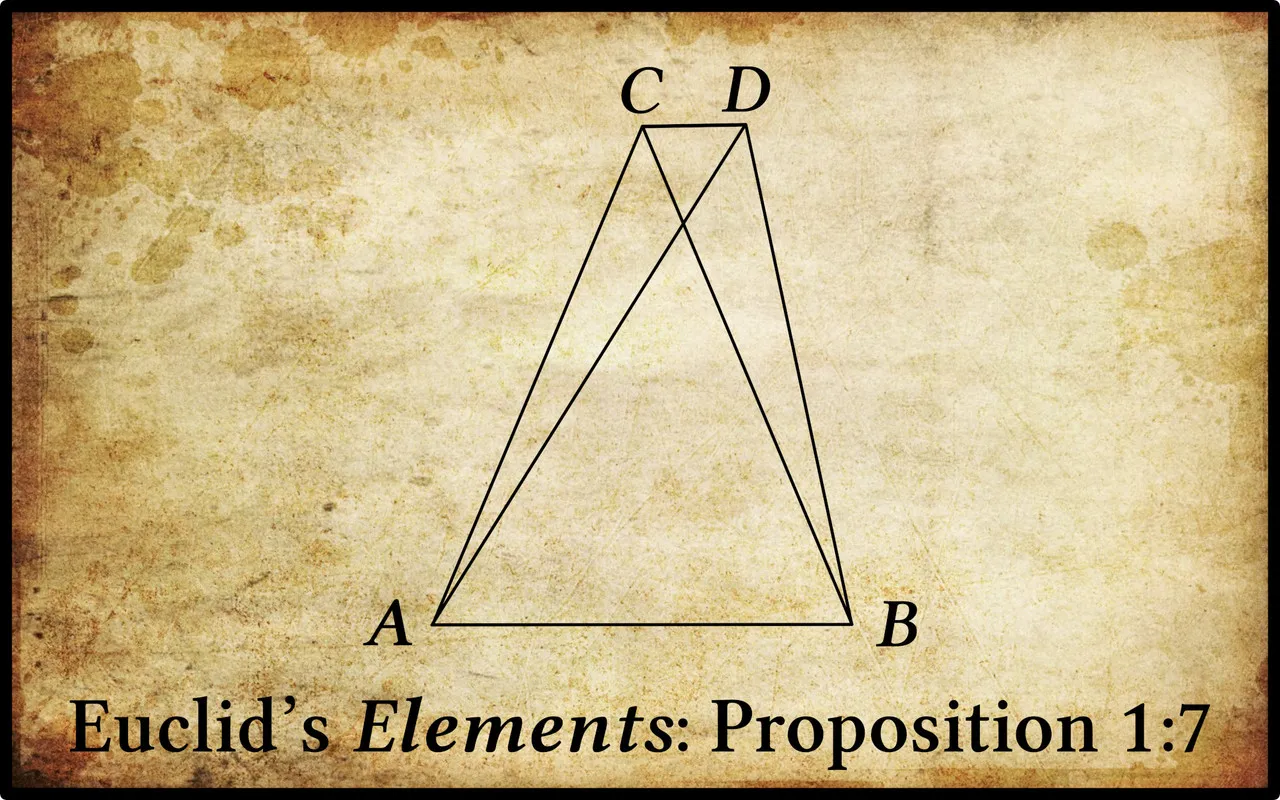
In Richard Fitzpatrick’s translation the seventh proposition of Book 1 of Euclid’s Elements reads:
| Greek | English |
|---|---|
| ̓Επὶ τῆς αὐτῆς εὐθείας δύο ταῖς αὐταῖς εὐθείαις ἄλλαι δύο εὐθεῖαι ἴσαι ἑκατέρα ἑκατέρᾳ οὐ συσταθήσονται πρὸς ἄλλῳ καὶ ἄλλῳ σημείῳ ἐπὶ τὰ αὐτὰ μέρη τὰ αὐτὰ πέρατα ἔχουσαι ταῖς ἐξ ἀρχῆς εὐθείαις. | On the same straight-line, two other straight-lines equal, respectively, to two (given) straight-lines (which meet) cannot be constructed (meeting) at a different point on the same side (of the straight-line), but having the same ends as the given straight-lines. |
This is quite a mouthful to digest, even with Fitzpatrick’s parenthetical additions. Thomas Heath notes:
In an English translation of the enunciation of this proposition it is absolutely necessary, in order to make it intelligible, to insert some words which are not in the Greek. The reason is partly that the Greek enunciation is itself very elliptical, and partly that some words used in it conveyed more meaning than the corresponding words in English do. Particularly is this the case with οὐ συσταθήσονται ἐπὶ “there shall not be constructed upon,” since συνίστασθαι is the regular word for constructing a triangle in particular. Thus a Greek would easily understand συσταθήσονται ἐπὶ as meaning the construction of two lines forming a triangle on a given straight line as base; whereas to “construct two straight lines on a straight line” is not in English sufficiently definite unless we explain that they are drawn from the ends of the straight line to meet at a point. I have had the less hesitation in putting in the words “from its extremities” because they are actually used by Euclid in the somewhat similar enunciation of 1:21. ―Heath 259
What Euclid means is that, given a triangle ACB with base AB, it is not possible to construct another triangle with sides equal in length to AC and BC respectively other than the mirror image of ACB. In other words, there are only two points―C and the reflection of C in line AB―that allow you to create a triangle with base AB and sides of length AC and BC. This property is related to the fact that if two circles are constructed, one with centre A and radius AC and the other with centre B and radius BC, then these circles will intersect at two and only two points. A picture paints a thousand words:
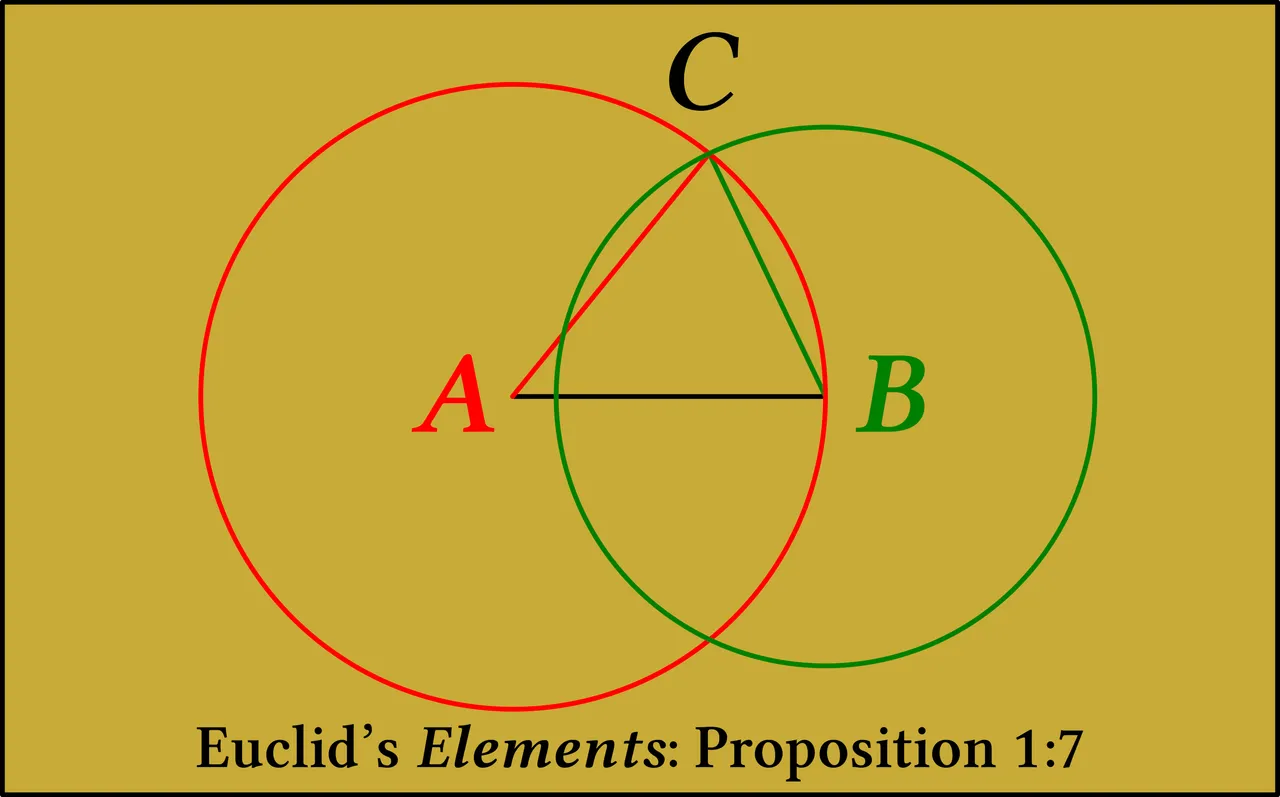
It is common for this proposition to be stated in a form that modern students find easier to understand. Heath quotes Robert Simson’s paraphrase, considering it to be the best:
Upon the same base, and on the same side of it, there cannot be two triangles that have their sides which are terminated in one extremity of the base equal to one another, and likewise those which are terminated at the other extremity. ―Heath 259 : Simson
Another version is that of the Irish encyclopaedist Dionysius Lardner, which may be expressed in modern terms as:
On a given line segment AB, there cannot be constructed on the same side two triangles ACB and ADB whose conterminous sides AC & AD and BC & BD are equal. ―Lardner 20 (adapted)
As Proclus points out in his Commentary (Morrow 206), this proposition is an example of what mathematicians call a lemma:
- lemma a lemma (plural: lemmas or lemmata) is a generally minor, proven proposition which is used as a stepping stone to a larger result. For that reason, it is also known as a helping theorem or an auxiliary theorem (Wikipedia)
Euclid requires this proposition in order to prove Proposition 1:8, the Side-Side-Side Congruence Theorem. Thomas Heath, however, believes that it has further application:
I have already referred (note on Proposition 1:1) to the mistake made by those editors who regard 1:7 as being of no use except to prove 1:8. What 1:7 proves is that if, in addition to the base of a triangle, the length of the side terminating at each extremity of the base is given, only one triangle satisfying these conditions can be constructed on one and the same side of the given base. Hence not only does 1:7 enable us to prove 1:8, but it supplements 1:1 and 1:22 [To construct a triangle out of three given line segments] by showing that the constructions of those propositions give one triangle only on one and the same side of the base. ―Heath 261
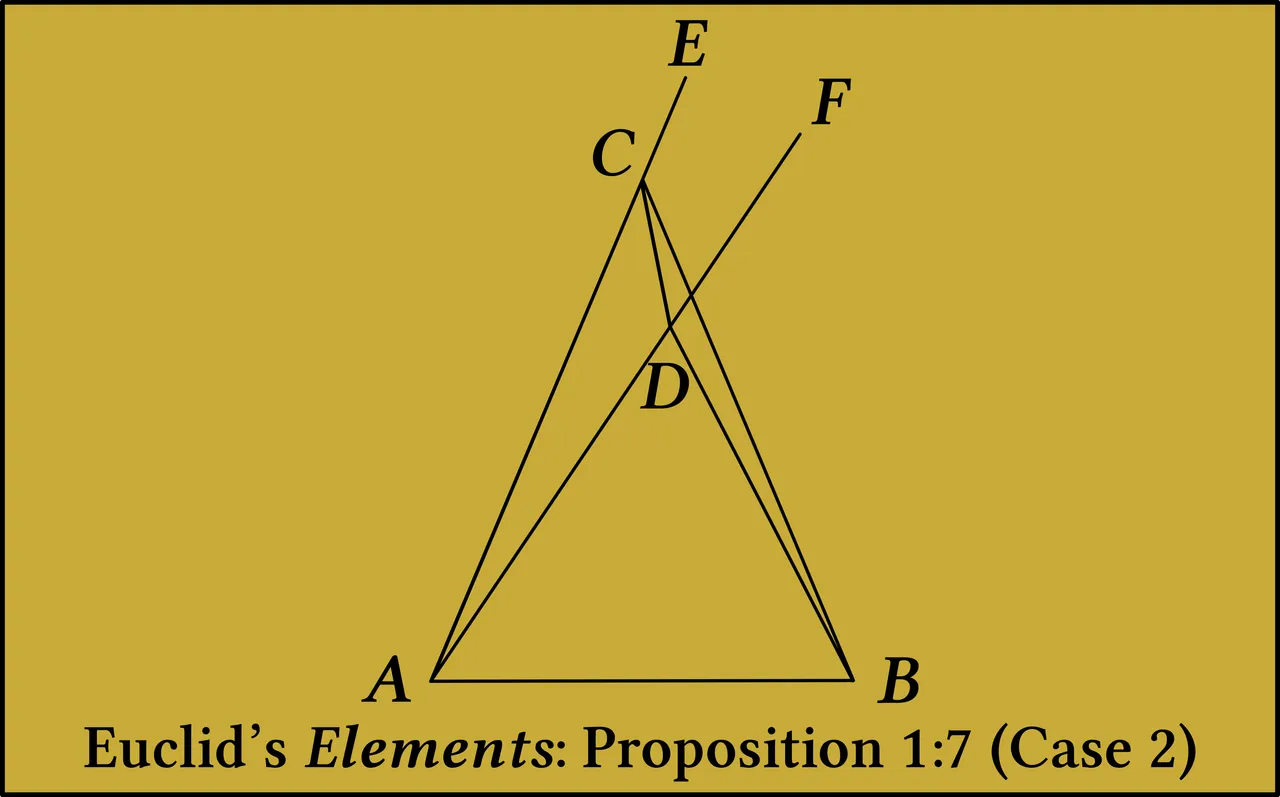
In his proof of 1:7 Euclid assumes that D lies outside triangle ABC. This proof needs to be modified in the case that D lies within triangle ABC. This is not the only time that Euclid only proves one of several possible cases. Over the millennia, commentators on the Elements have supplied proofs for the other cases that may arise. See, for example, Robert Simson’s proof, which relies on the second part of Proposition 1:5: The external angles below the base of an isosceles triangle are equal in measure (Simson 12 : Heath 260).
Euclid’s proof of 1:7 relies on the following premises (I exclude the definitions):
Postulate 1 To draw a straight line from any point to any point.
Proposition 1:5 The angles at the base of an isosceles triangle are equal in measure.
Common Notion 5 The whole is greater than the part.
Euclid’s proof also relies upon a number of assumptions or axioms that are not listed among his Common Notions:
If x < y and y = z, then x < z.
If x < y and y < z, then x < z.
Euclid proves this theorem by reductio ad absurdum: he assumes that it is possible to construct two triangles on the same side of AB with corresponding sides equal, and then shows how this leads to a contradiction. In modern terminology the proof of the theorem may be stated as follows:

Proclus on Eclipses
In his Commentary on the First Book of Euclid’s Elements, Proclus claims that Proposition 1:8 can be easily proved without having recourse to Proposition 1:7. Why then did Euclid include 1:7?
Was it not, then, superfluous, they say, for the author of the Elements to introduce it? For if it was only for the sake of the eighth that we brought it in, and if the eighth can be demonstrated without it, is not the seventh manifestly useless?
To this we must reply, as others have done before us, that the demonstration of the seventh is of the greatest utility to astronomers in the area of eclipses. For by the use of this theorem they say they can show that three successive eclipses cannot occur at equal intervals from one another, that is, the third separated from the second by the same interval of time as the second from the first. For example, if the second has occurred six months and twenty days after the first, the interval before the third occurs cannot be this length of time but must be either longer or shorter. They say that this is demonstrated to be the case by the seventh theorem, and that this is not the only theorem the author of the Elements has demonstrated because it contributes to astronomy as a secondary aim, but many other theorems and problems as well. ―Morrow 209–210
Is this true? How on earth did the ancient Greeks use Proposition 1:7 to deduce this fact? I am not the only one to be mystified by this remark:
It is also interesting to see how little insight a prominent scholar in the fifth century A.D. had into the character and purpose of early Greek science. Proclus seriously believes that much of Euclid’s “Elements” was developed because of its utility for astronomy ... One such postulated connection between an Euclidean theorem and astronomy remains obscure. Proclus says that Euclid 1:7, a congruence theorem for triangles [Heath 258–261], had been used to prove that no two consecutive intervals between eclipses can be equal [Morrow 209 f]. In this general formulation the statement is obviously wrong but the numerical example that mentions two consecutive intervals of 6 months and 20 days [Probably 6m 20d (= 200d ) is some mistake (177 + 29?).] is correct insofar as the first and the third eclipse would be separated by more than 13 months and this is impossible. ―Neugebauer 1034–1035

And that’s a good place to stop.
References
- Ernst Ferdinand August, Euclidis Elementa, Part 1, Theodor Trautwein, Berlin (1826)
- Henry Billingsley (translator), The Elements of Geometrie of the Most Auncient Philosopher Evclide of Megara, John Day, London (1582)
- Oliver Byrne, The First Six Books of The Elements of Euclid in Which Coloured Diagrams and Symbols Are Used Instead of Letters for the Greater Ease of Learners, William Pickering, London (1847)
- Richard Fitzpatrick (translator), Euclid’s Elements of Geometry, University of Texas at Austin, Austin, TX (2008)
- Thomas Little Heath (translator & editor), The Thirteen Books of Euclid’s Elements, Second Edition, Volume 1, Dover Publications, New York (1956)
- Johan Ludvig Heiberg, Heinrich Menge, Euclidis Elementa edidit et Latine interpretatus est I. L. Heiberg, Volumes 1-5, B G Teubner Verlag, Leipzig (1883-1888)
- Dionysius Lardner, The First Six Books of the Elements of Euclid, Taylor & Walton, London (1828)
- Henry George Liddell, Robert Scott, A Greek-English Lexicon, Eighth Edition, American Book Company, New York (1901)
- Glenn Raymond Morrow (translator), Proclus: A Commentary on the First Book of Euclid’s Elements, Princeton University Press, Princeton, NJ (1970)
- François Peyrard, Les Œuvres d’Euclide, en Grec, en Latin et en Français, Volumes 1-3, Charles-Frobert Patris, Paris (1814, 1816, 1818)
- Robert Simson, The Elements of Euclid, F Wingrave, London (1804)
- Thomas Taylor, The Philosophical and Mathematical Commentaries of Proclus on the First Book of Euclid’s Elements, Volume 1, Volume 2, London (1792)
Image Credits
- Otto Neugebauer: Anonymous Photographer, Mathematisches Institut, Georg-August-Universität Göttingen, Public Domain
Online Resources
