In Book 1 of Euclid’s Elements, the first of the Five Common Notions reads (Fitzpatrick 7):
| Greek | English |
|---|---|
| αʹ. Τὰ τῷ αὐτῷ ἴσα καὶ ἀλλήλοις ἐστὶν ἴσα. | 1. Things equal to the same thing are also equal to one another. |
As we saw in the last article, David Joyce understands Euclid’s things to refer to magnitudes of various forms:
These common notions, sometimes called axioms, refer to magnitudes of one kind. The various kinds of magnitudes that occur in the Elements include lines, angles, plane figures, and solid figures. (Joyce)
An earlier commentator on the Elements, Proclus, takes a broader view, but in the following passage he probably means that geometers apply the Common Notions to magnitudes while other scientists apply them to other quantities:
These axioms are common, but each individual uses them with reference to his specific subject-matter and to the extent which his subject-matter demands. One man applies them to magnitudes, another to numbers, another to intervals of time. In this way, although the axioms are general, they lead to specific conclusions in each science. (Morrow 154)

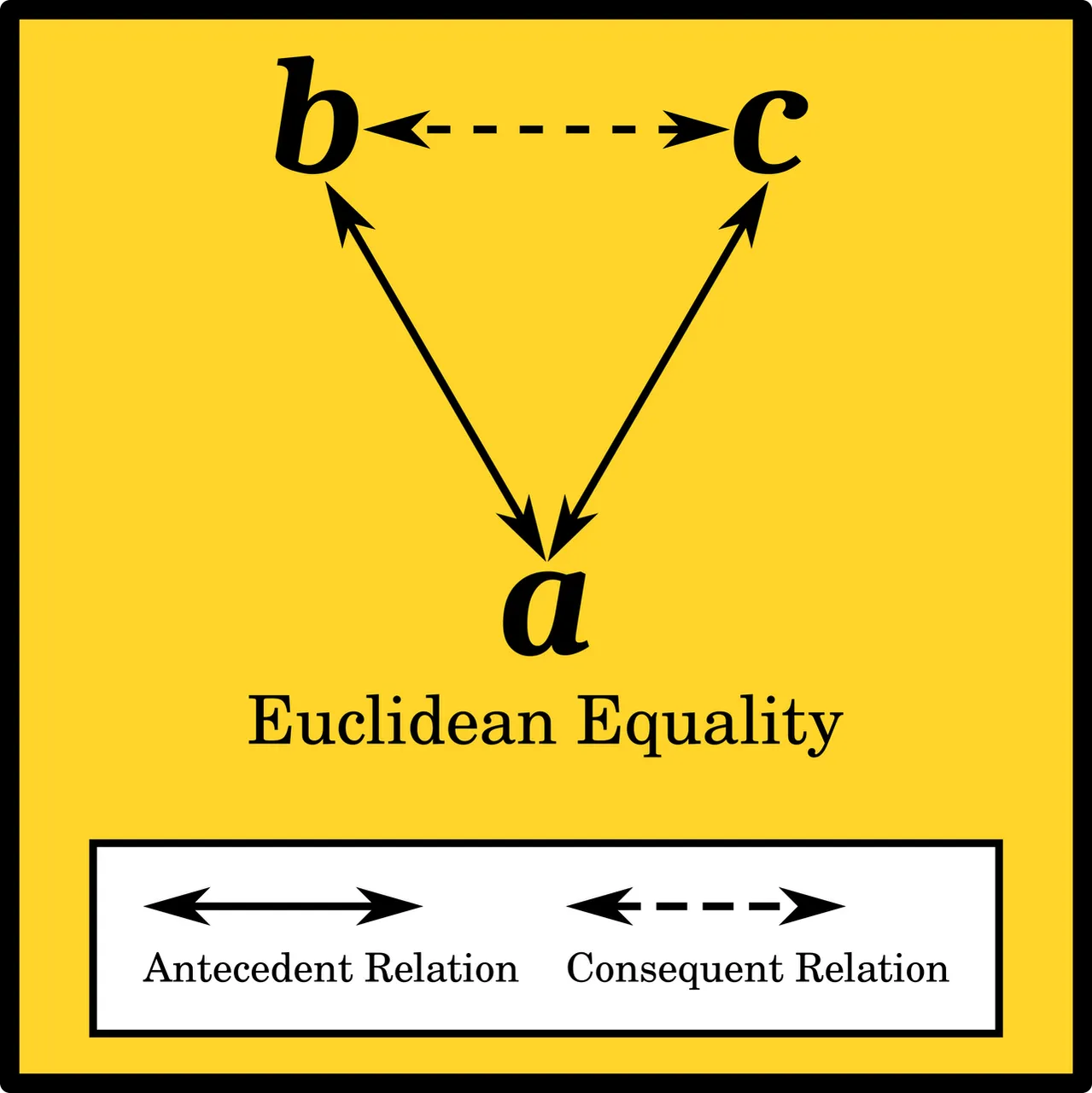
Euclidean Equality
In the context of geometry, we sometimes use the word congruent to convey the idea of equality in geometry:
Two line segments are congruent if they have the same length.
Two angles are congruent if they have the same measure.
But Euclid also uses Common Notion 1 to prove, for example, that two parallelograms are equal (1:36), or that two triangles are equal (1:37), or even that a parallelogram is equal to a triangle (1:42). In these cases he means that the areas of these figures are the same. This is not congruence, which would require that the two figures also have the same shape.
It should be appreciated, however, that Euclid’s concepts of area and volume were quite different from ours:
It is well known that Euclid had no conception of area or volume in the modern sense and made no use of numbers in order to express the measure of things. Rather, in order to “measure” figures, Euclid transformed a figure into another figure equivalent to it (i.e., in modern terms, with the same area or volume) having a standard shape—generally a parallelogram or a square. (De Risi 11)
In modern mathematics Euclidean Equality is defined as a binary relation that associates an element of one set with an element of the same or another set. Euclid, however, never defines equality in the Elements. Set theory is alien to his geometry, and he never explicitly restricts equality to two things at a time. Nevertheless, from his use of the term in both the axioms (Postulate 4 and Common Notions 1-4) and the propositions it is reasonable to assign the following properties to Euclidean Equality:
It is a binary relation: it relates one thing to another thing.
It is a symmetric relation: a = b ⇔b = a.
The first of these, however, may be questioned. In Proposition 1:1, for example, Euclid writes:
And since the point A is the center of the circle CDB, AC is equal to AB [Def. 1.15]. Again, since the point B is the center of the circle CAE, BC is equal to BA [Def. 1.15]. But CA was also shown (to be) equal to AB. Thus, CA and CB are each [ἑκατέρα] equal to AB. But things equal to the same thing are also equal to one another [C.N. 1]. Thus, CA is also equal to CB. Thus, the three (straight-lines) CA, AB, and BC are equal to one another. (Fitzpatrick 8)
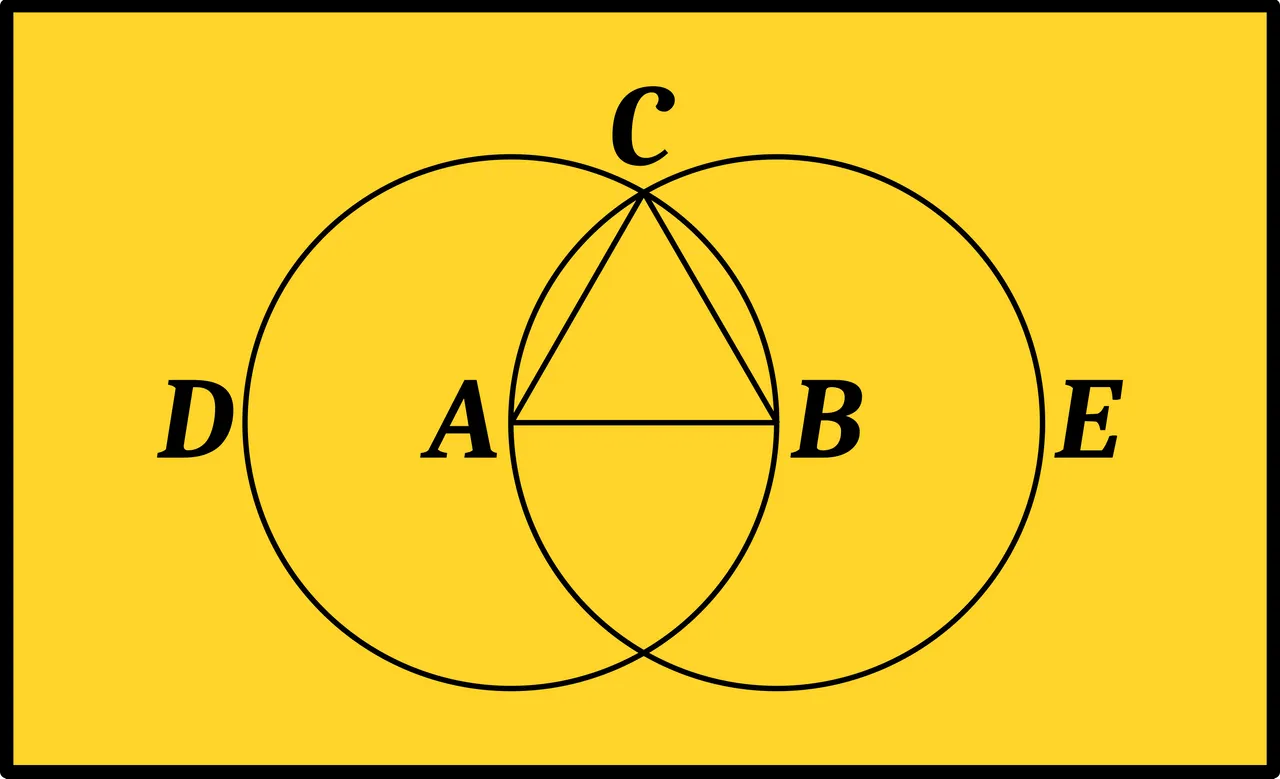
Note how Euclid is careful to include the word each [ἑκατέρα] when stating that CA and CB are each equal to AB. But in his final conclusion he is happy to regard equality as a ternary relation. This is, however, very much the exception. The next time he does something similar is in Proposition 1:46, where he concludes: Thus, the four (sides) BA, AD, DE, and EB are equal to one another, making equality a quaternary relation (Fitzpatrick 45). There are only a dozen or so places in the Elements where Euclid equates three, four, five or six things at a time: Propositions 2:8, 3:25, 4:9, 4:10, 4:12, 4:13, 4:14, 4:15, 6:1, 7:15, 11:23, 11:25, 12:13, 13:13, 13:14 and 13:17. For every one of these exceptions there are literally dozens of cases where equality is strictly a binary relation.
It is sometimes said that Common Notion 1 expresses the transitive property of relations. For example, the transitive relation involving the lengths—a, b and c—of three line segments and the relation equality takes the following form:
- If a = b and b = c then a = c.
But this is not precisely equivalent to Euclid’s Common Notion 1. To deduce transitivity from Common Notion 1 we also require that equality be a symmetric relation:
- If a = b then b = a.
Of course, equality is symmetric, but Euclid never states this explicitly—he merely assumes it.
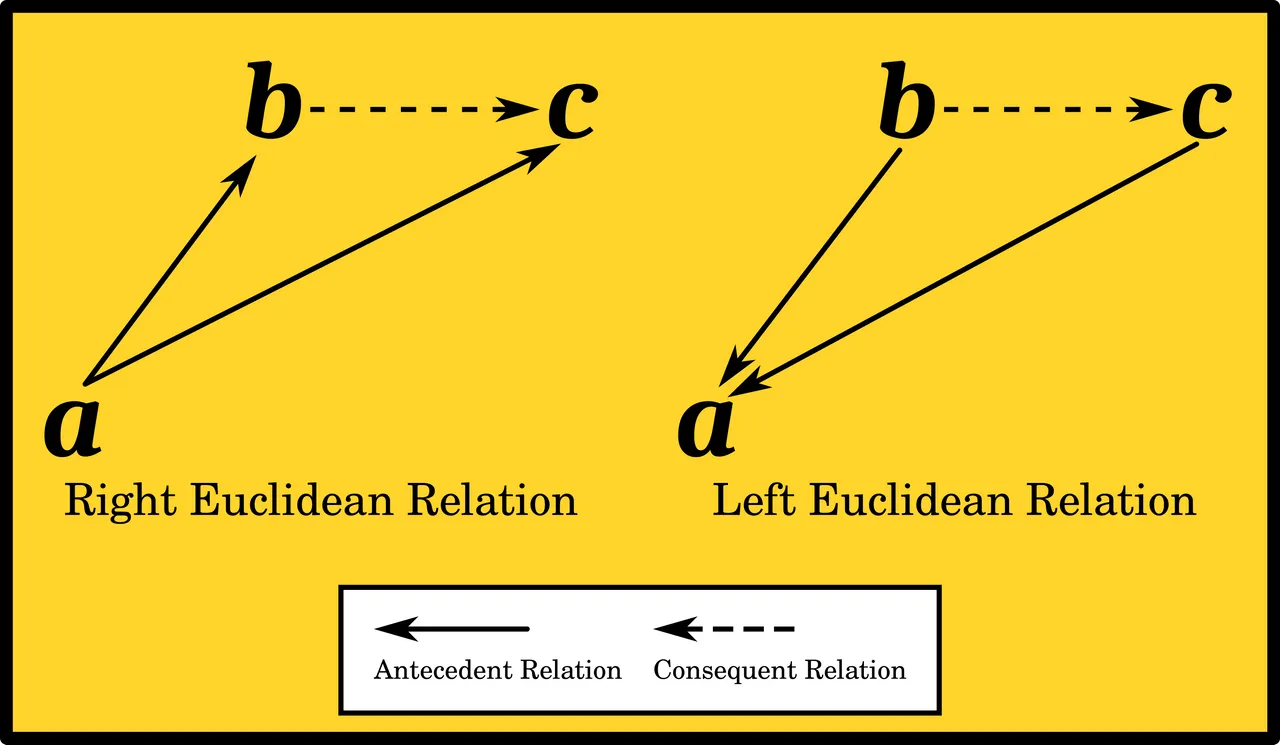
Modern mathematicians have actually defined a Euclidean Relation, which formalizes Euclid’s Common Notion 1. A Euclidean Relation is any relation which has the property: Things which are related to the same thing are related to each other.
To express this more formally:
A binary relation R on a set X is Right Euclidean if it satisfies the following condition: for every a, b, c in X, if a is related to b and a is related to c, then b is related to c:
A binary relation R on a set X is Left Euclidean if it satisfies the following condition: for every a, b, c in X, if b is related to a and c is related to a, then b is related to c:
For symmetric relations, transitivity, right Euclideanness, and left Euclideanness all coincide. As we have seen, Euclidean Equality is a symmetric relation.
Euclid’s Use of Common Notion 1
In the course of the Elements, Euclid rarely cites this Common Notion explicitly when proving a proposition. In Proposition 1:1, the very first theorem in the book, he invokes it to demonstrate that two line segments are of equal length. On other occasions, he uses it without explicitly invoking it—for example, in Proposition 1:3. Here is a comprehensive list of all the times Euclid either explicitly or implicitly cites Common Notion 1 (I exclude cases where the proof of one proposition depends on the proof of an earlier proposition that used Common Notion 1):
| Proposition | Things | Explicit? |
|---|---|---|
| 1:1 | line segments | Yes |
| 1:2 | line segments | Yes |
| 1:3 | line segments | No |
| 1:13 | sums of angles | Yes |
| 1:14 | sums of angles | No |
| 1:15 | sums of angles | No |
| 1:22 | line segments | No |
| 1:26 | angles | No |
| 1:28 | angles, sums of angles | No |
| 1:29 | angles | No |
| 1:30 | angles | No |
| 1:32 | sums of angles | No |
| 1:35 | line segments | No |
| 1:36 | areas | No |
| 1:37 | areas | No |
| 1:39 | angles | No |
| 1:40 | areas | No |
| 1:42 | areas | No |
| 1:44 | areas | No |
| 1:45 | angles | No |
| 1:47 | areas | No |
| 1:48 | areas | No |
| 2:10 | areas | No |

In Propositions 1:15 and 1:32 Euclid equates something to “two right angles”. Thomas Heath, in his commentary on Proposition 1:15, cites Common Notion 1 in support of this (Heath 278), but Ian Mueller, a scholar of Greek philosophy and mathematics, has expressed doubts in a paper he wrote on Proposition 1:32:
So Heath (1926, 278), but normally the common notion is applied to “things,” specific magnitudes like lines or angles or triangles, and not to more abstract quantities like “two right angles.” It seems to me possible that Euclid is simply taking for granted that if all right angles are equal [Postulate 4] then things equal to two right angles are equal to each other. But nothing I say in this essay turns on this question. (Mueller 295 fn 13)
In Proposition 1:37 the areas of two triangles are each half the area of a given parallelogram, and therefore they are said to be equal to each other. In Propositions 1:42 and 1:47 two areas are each twice the area of equal areas, and therefore they are said to be equal to each other. I think these cases can be regarded as applications of Common Notion 1. But in the last article we saw how some manuscripts of the Elements include these cases as explicit Common Notions in their own right:
| Heiberg | Greek | English |
|---|---|---|
| V | Καὶ τὰ τοῦ αὐτοῦ διπλάσια ἴσα ἀλλήλοις ἐστίν. | And those things which are equal to twice the same thing are equal to each other. |
| VI | Καὶ τὰ τοῦ αὐτοῦ ἡμίση ἴσα ἀλλήλοις ἐστίν. | And those things which are equal to half the same thing are equal to each other. |
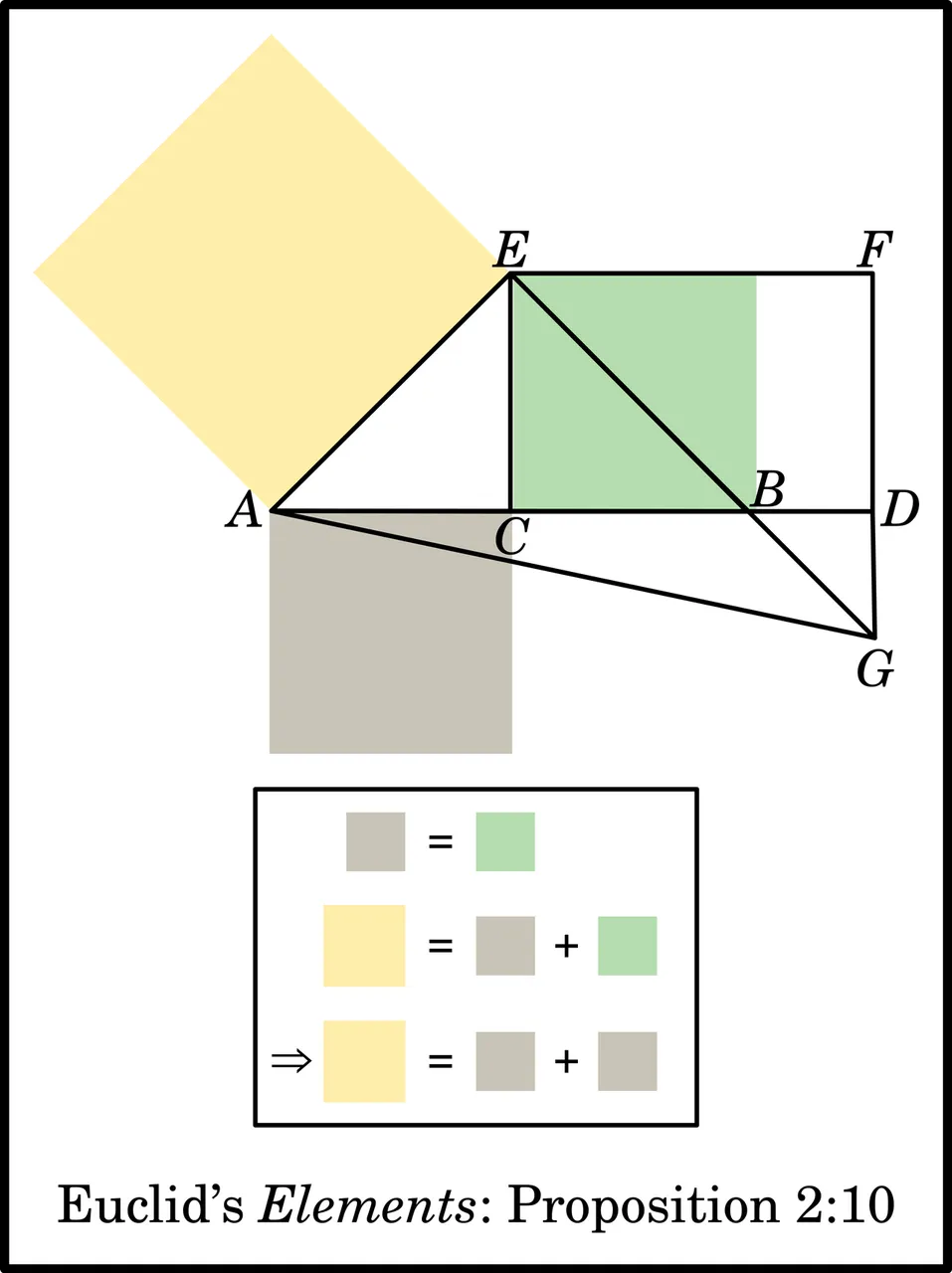
The Elements is a carefully structured work, with the proofs of later propositions being built upon those of earlier, more fundamental propositions. One of the consequences of this is that the explicit use of Common Notion 1 is virtually absent after Book 1. Proposition 2:10 is the only instance cited by Thomas Heath, though David Joyce does not invoke any of the Common Notions in the proof of this proposition. It is another borderline case: one area is shown to be equal to the sum of two other areas : but those two other areas are known to be equal to each other : therefore the first area is equal to twice the second of the two other areas.
In truth, though, Common Notion 1 is almost ubiquitous throughout the later geometric books of the Elements, but it is buried, as it were, in the foundations of the proofs.
Note also that Book 5, Proposition 11 reads:
(Ratios which are) the same with the same ratio are also the same with one another. (Fitzpatrick 141)
As David Joyce points out, this statement is analogous to Common Notion 1 for magnitudes. The fact that this is a proposition, which Euclid proceeds to prove, demonstrates that Common Notion 1 certainly does not apply to ratios—whatever else it might apply to.
And that’s a good place to stop.
References
- Ernst Ferdinand August, Euclidis Elementa, Part 1, Theodor Trautwein, Berlin (1826)
- Henry Billingsley (translator), The Elements of Geometrie of the Most Auncient Philosopher Evclide of Megara, John Day, London (1582)
- Richard Fitzpatrick (translator), Euclid’s Elements of Geometry, University of Texas at Austin, Austin, TX (2008)
- Thomas Little Heath (translator & editor), The Thirteen Books of Euclid’s Elements, Second Edition, Dover Publications, New York (1956)
- Johan Ludvig Heiberg, Heinrich Menge, Euclidis Elementa edidit et Latine interpretatus est I. L. Heiberg, Volumes 1-5, B G Teubner Verlag, Leipzig (1883-1888)
- Henry George Liddell, Robert Scott, A Greek-English Lexicon, Eighth Edition, American Book Company, New York (1901)
- Glenn Raymond Morrow (translator), Proclus: A Commentary on the First Book of Euclid’s Elements, Princeton University Press, Princeton, NJ (1970)
- Ian Mueller, Remarks on Euclid’s Elements I,32 and the Parallel Postulate, Science in Context, Volume 16, Issue 3, Pages 287-297, Cambridge University Press, Cambridge (2003)
- François Peyrard, Les Œuvres d’Euclide, en Grec, en Latin et en Français, Volumes 1-3, Charles-Frobert Patris, Paris (1814, 1816, 1818)
- Vincenzo De Risi, Euclid’s Common Notions and the Theory of Equivalence, Foundations of Science, Volume 26, Issue 2, Pages 301-324, Springer Science+Business Media, Berlin (2021)
- Thomas Taylor, The Philosophical and Mathematical Commentaries of Proclus on the First Book of Euclid’s Elements, Volume 1, Volume 2, London (1792)
Image Credits
- Euclid, Common Notion 1: Jusepe di Ribera (artist), Getty Center, Los Angeles, Public Domain
- Ian Mueller: © Lloyd DeGrane (photographer), The University of Chicago Photographic Archive, Hanna Holborn Gray Special Collections Research Center, University of Chicago Library, Creative Commons License
Online Resources
