Cryptographic Hash Functions
The first cryptographic primitive that we’ll need to understand is a cryptographic hash function.A hash functionis a mathematical function with the following three properties:
● Its input can be any string of any size.
● It produces a fixed size output. For the purpose of making the discussion in this chapter concrete, we will assume a 256-bit output size. However, our discussion holds true for any output size as long as it is sufficiently large.
● It is efficiently computable. Intuitively this means that for a given input string, you can
out what the output of the hash function is in a reasonable amount of time. More technically, computing the hash of an n-bit string should have a running time that is O(n).
Those properties define a general hash function, one that could be used to build a data structure such as a hash table. We’re going to focus exclusively on cryptographichash functions. For a hash function to be cryptographically secure, we’re going to require that it has the following three additional properties: (1) collision-resistance, (2) hiding, (3) puzzle-friendliness.
We’ll look more closely at each of these properties to gain an understanding of why it’s useful to have a function that behaves that way. The reader who has studied cryptography should be aware that the treatment of hash functions in this book is a bit different from a standard cryptography textbook. The puzzle-friendliness property, in particular, is not a general requirement for cryptographic hash functions, but one that will be useful for cryptocurrencies specifically.
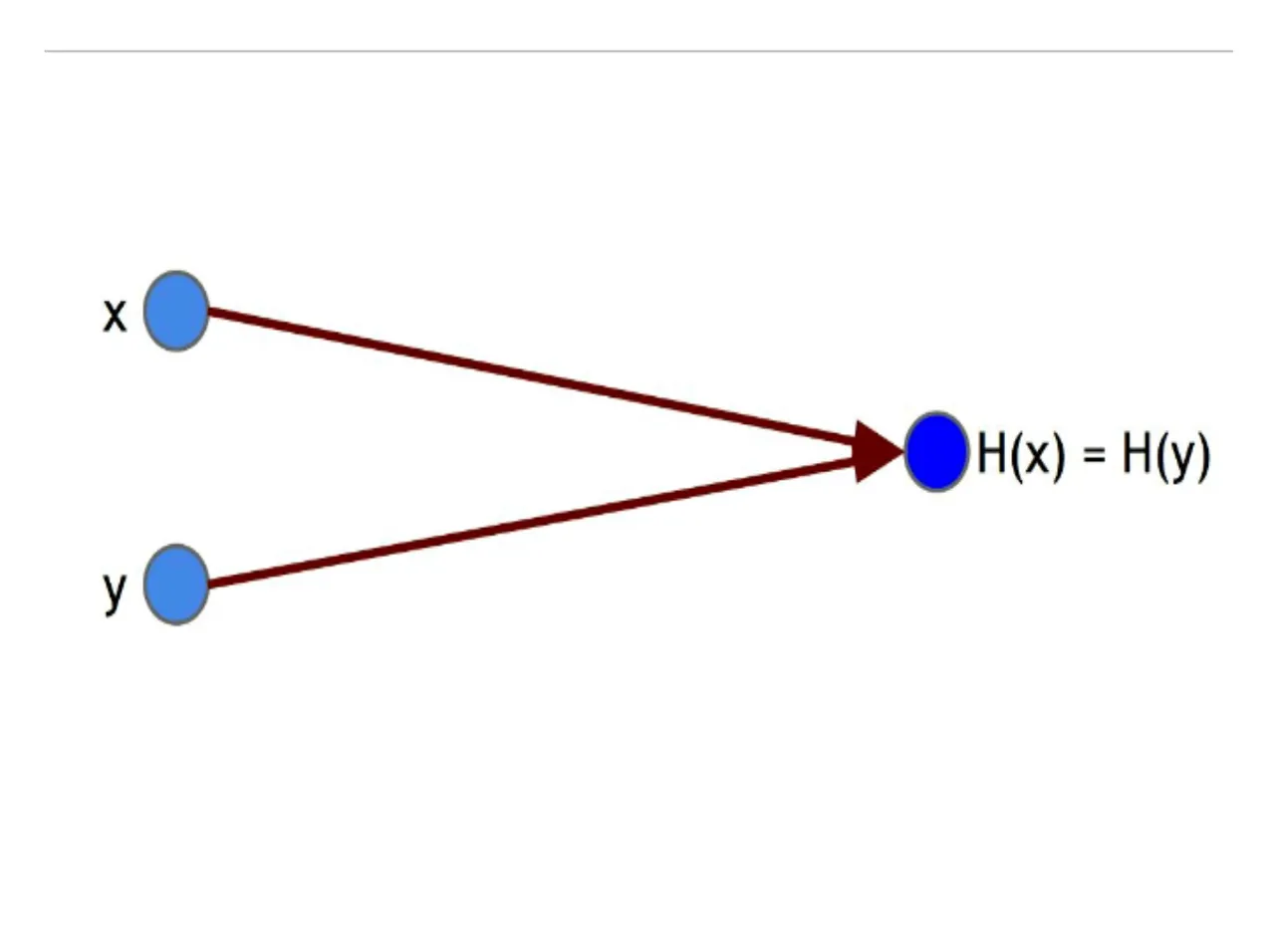
Property 1: Collision-resistance.The first property that we need from a cryptographic hash function is that it’s collision-resistant. A collision occurs when two distinct inputs produce the same output. A hash function H(.) is collision-resistant if nobody can find a collision. Formally:
Collision-resistance: A hash functionHis said to be collision resistant if it is infeasible to findtwo values, xand y, such that x ≠y, yet H(x)=H(y).
Figure 1.1 A hash collision. x and yare distinct values, yet when input into hash function H, they produce the same output.
Notice that we said nobody can find a collision, but we did not say that no collisions exist. Actually, we know for a fact that collisions do exist, and we can prove this by a simple counting argument. The input space to the hash function contains all strings of all lengths, yet the output space contains only strings of a specific fixed length. Because the input space is larger than the output space (indeed, the input space is infinite, while the output space is finite), there must be input strings that map to the same output string. In fact, by the Pigeonhole Principle there will necessarily be a very large number of possible inputs that map to any particular output.