Haskell has a maximum function and it has lazy evaluations of lists. I come from Python that has a max function and list generators. But there turns out to be a crucial difference.
Day 11 asks us to find maximum-value squares in a programatically defined integer array. Part 1 asks for 3x3 squares so I (foolishly) built something that only worked for 3x3 squares.
Puzzle input is a "serial number" so I made a function that when partially applied to the serial number gives the function x, y -> value of the cell.
type LevelFunction = Int -> Int -> Int
fuelCellLevel :: Int -> LevelFunction
fuelCellLevel serialNumber y x =
let rackId = (x+10)
allDigits = (rackId * y + serialNumber) * rackId in
((allDigits `div` 100) `mod` 10) - 5
I felt the key here was going to be avoiding redundant calls to this function, as well as adding the same numbers over and over again. My solution for part 1 was to add three rows together:
1 2 3 4 5 ...
6 7 8 9 10 ...
11 12 13 14 15 ...
-------------------
18 21 24 27 30 ...
and then take units of three to get the sum of all the 3x3 squares. In order to keep track of where the square came from, we need to have both a sum and a label.
Generate an entire row of values:
gridRange = [1..300]
rowLevels fn y = (map (fn y) gridRange)
Some utility functions for operating on tuples:
sum3 (a,b,c) = a + b + c
sumColumns (y,as,bs,cs) =
(y, map sum3 (zip3 as bs cs))
sumSquare y (x,a,b,c) = (a+b+c, x, y)
Take the rows three at a time and add them up in the way shown above. The zip functions all use the shortest list length. Using zip this way is a common Python idiom, I don't know if Haskell people do it too or if they have a different preferred way of accomplishing it.
threeByThreeLevels :: (Int -> Int -> Int) -> [(Int,Int,Int)]
threeByThreeLevels fn =
let rows = [ rowLevels fn y | y <- gridRange ] :: [[Int]]
threeRows = zip4 gridRange rows (drop 1 rows) (drop 2 rows) :: [(Int,[Int],[Int],[Int])]
threeRowsSummed = map sumColumns threeRows in
concat (map sumSquares threeRowsSummed)
Then the same pattern is used to take the columns three at a time:
sumSquares :: (Int,[Int]) -> [(Int,Int,Int)]
sumSquares (y,cols) =
let threeCols = zip4 gridRange cols (drop 1 cols) (drop 2 cols) in
map (sumSquare y) threeCols
We ordered things so that the sum comes first in the tuple, so we can just apply maximum to the tuples as they are:
maxSquare serialNumber = maximum (threeByThreeLevels (fuelCellLevel serialNumber))
OK, that works for part 1. Part 2 asks us to find the maximum-valued square of any size, so all that work was wasted.
I thought about it a bit and decided the right solution was inclusion/exclusion. Suppose we know, for every point (m,n) in the array, the value of the sum of all the entries between (1,1) and (m,n). Then we can calculate the value of any smaller rectangle by doing some math.
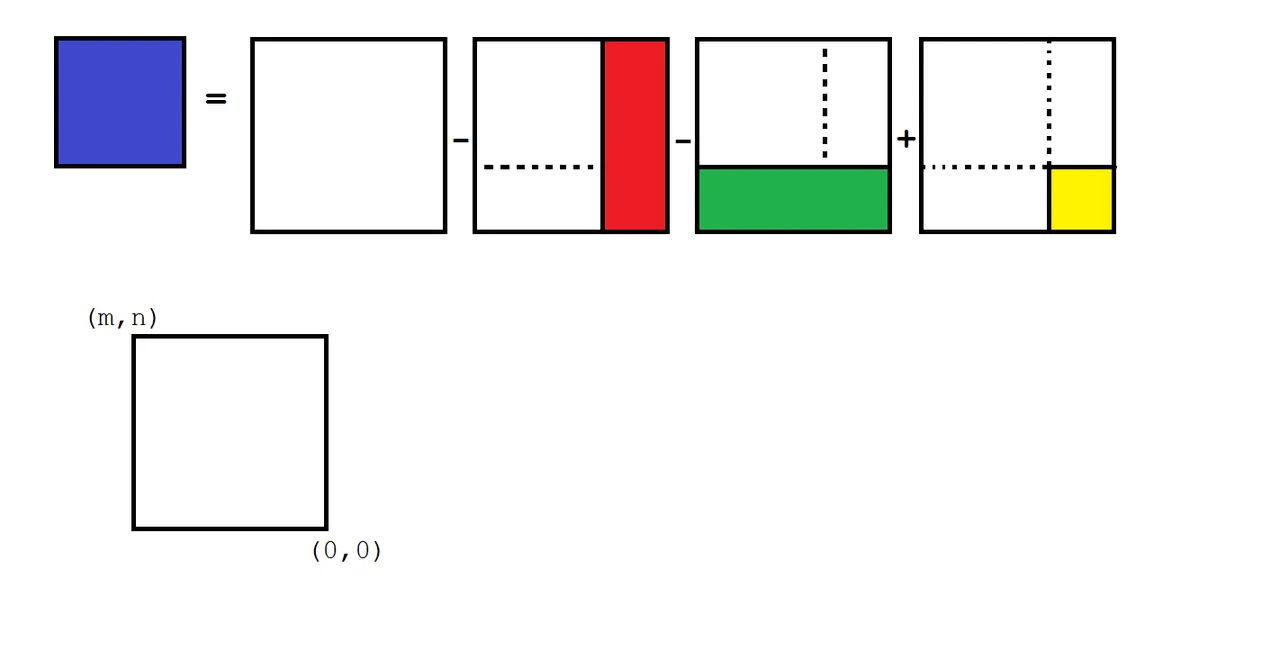
We want the area of a small blue square not beginning at (1,1). So, we can start with the big sum (white square), subtract off the portion on the right that we don't want (red rectangle) and the portion on the bottom that we don't want (green rectangle.) That means part of the original area got subtracted twice, so we have to add that back in (yellow.)
This technique allows us to precompute a matrix of all the area sums that start at (1,1), and then compute any other sum with just four references into this array.
The code I wrote is a little magical, but follows one of the examples given in
Data.Array. We can refer back to the array in order to define it! Here I do this twice, once to define columns in terms of earlier columns (and the previous row), and once to define the rows of the matrix in terms of its earlier rows:
-- Return an entire row's worth of sums
rowPartialSums :: LevelFunction -> Int -> Array Int Int -> Array Int Int
rowPartialSums fn y prevRow =
let a = array (1,300) ((1, (prevRow!1) + fn y 1) :
[(x, (a!(x-1)) + (prevRow!x) + (fn y x) - (prevRow!(x-1))) | x <- [2..300] ]) in a
-- Entire matrix of sums, (array ! y) ! x = sum from (1,1) to (y,x)
partialSums :: LevelFunction -> Array Int (Array Int Int)
partialSums fn =
let zero = array (1,300) [(x,0) | x <- [1..300]]
rows = array (1,300) ((1, rowPartialSums fn 1 zero) :
[(y, rowPartialSums fn y (rows!(y-1))) | y <- [2..300] ]) in rows
sums serialNumber = partialSums (fuelCellLevel serialNumber)
If you look at rowPartialSums it's doing inclusion-exclusion here too. We want to define A[x][y] in terms of sums we already know. So it's equal to fn(x,y) + A[x-1][y] + A[x][y-1], but both those values already include the value of A[x-1][y-1].
I see looking at this that I could have curried fn which was my intention for putting y first, but I didn't.
Now to do the inclusion-exclusion, we need to be careful of the edge cases, so I just wrote everything out in four big cases and didn't worry too much about making it compact:
areaSum :: Array Int (Array Int Int) -> Int -> Int -> Int -> Int
areaSum a 1 1 size = let
x' = size
y' = size in
(a ! y') ! x'
areaSum a 1 x size = let
x' = x + size - 1
y' = size in
(a ! y') ! x' - (a ! y') ! (x-1)
areaSum a y 1 size = let
x' = size
y' = y + size - 1 in
(a ! y') ! x' - (a ! (y-1)) ! x'
areaSum a y x size = let
x' = x + size - 1
y' = y + size - 1 in
(a ! y') ! x' - (a ! (y-1)) ! x' - (a ! y') ! (x-1) + (a ! (y-1)) ! (x-1)
OK, just one more step and we're done, right? We just have to iterate over all sizes and all locations where squares of that sizes could fit, which we can do in one big list comprehension:
maxSquareK :: Int -> (Int,Int,Int,Int)
maxSquareK sn = let a = sums sn in
maximum [ (areaSum a y x size, x, y, size) |
size <- [1..300],
x <- [1..301-size],
y <- [1..301-size] ]
Oops, doesn't work: day11.hs: stack overflow
OK, time to try profiling. We can compile the program with profiling enabled like this:
mark@ubuntu:~/aoc2018/day11$ stack ghc -- -prof -fprof-auto -fprof-cafs day11.hs
[1 of 1] Compiling Main ( day11.hs, day11.o )
Linking day11 ...
And run it like this to get heap profiling:
mark@ubuntu:~/aoc2018/day11$ ./day11 +RTS -hc -p
This results in a test file full of samples like this one:
BEGIN_SAMPLE 0.919256
(150)GHC.IO.Handle.Text.CAF 24
(241)CAF:$dShow_r3Z2 152
(126)PINNED 36816
(249)main 120
(248)main/CAF:main 96
MAIN 160
(233)GHC.Conc.Signal.CAF 640
(212)GHC.IO.Handle.FD.CAF 704
(220)GHC.IO.Encoding.Iconv.CAF 120
(222)GHC.IO.Encoding.CAF 1096
(277)maxSquareK/main/CAF:main 301482248
END_SAMPLE 0.919256
OK, that's a lot of memory allocation, but why?
individual inherited
COST CENTRE MODULE SRC no. entries %time %alloc %time %alloc
...
maxSquareK Main day11.hs:(91,1)-(95,32) 277 1 41.1 47.3 81.2 70.4
areaSum Main day11.hs:(66,1)-(84,75) 278 967107 30.8 18.7 36.6 21.1
areaSum.y' Main day11.hs:83:3-19 295 960306 2.8 1.2 2.8 1.2
areaSum.x' Main day11.hs:82:3-19 296 960305 3.0 1.2 3.0 1.2
areaSum.x' Main day11.hs:77:3-11 286 3522 0.0 0.0 0.0 0.0
areaSum.y' Main day11.hs:78:3-19 283 3522 0.0 0.0 0.0 0.0
areaSum.x' Main day11.hs:72:3-19 294 3267 0.0 0.0 0.0 0.0
areaSum.y' Main day11.hs:73:3-11 293 3267 0.0 0.0 0.0 0.0
areaSum.x' Main day11.hs:67:3-11 292 12 0.0 0.0 0.0 0.0
areaSum.y' Main day11.hs:68:3-11 291 12 0.0 0.0 0.0 0.0
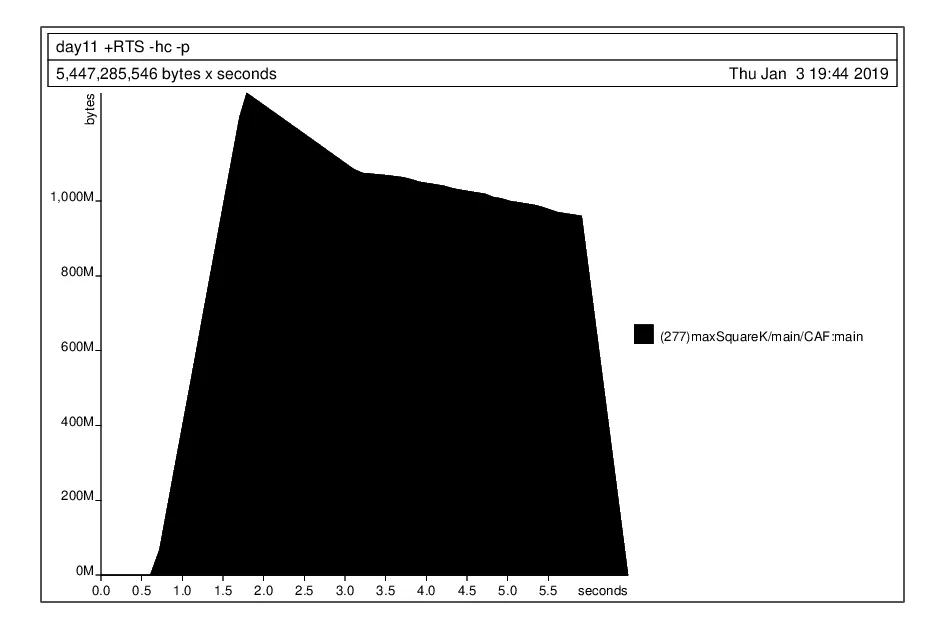
I find this a little confusing; it looks like we're accumulating a lot of memory in areaSum. Actually, we're accumulating a bunch of unevaluated areaSum thunks.
The reason is that maximum doesn't do what I thought, which is to do a strict fold. Instead it does lazy evaluation of the entire list of comparisons, as if the intermediate result was
max( a, max( b, max( c, max( d, ... ) ) ) )
where each of the arguments is one of the areaSum function calls. I have no idea why this is the preferred default behavior. It also suggests that part 1 is using way too much memory as well. If you plot it memory usage does start going down, eventually, when we reach the end of the large list generated by the comprehension.
OK, quick hack. We'll use foldl' which uses strict evaluation (doesn't defer the comparison) like this:
maximum' = foldl' max (0,0,0,0)
maxSquareK :: Int -> (Int,Int,Int,Int)
maxSquareK sn = let a = sums sn in
maximum' [ (areaSum a y x size, x, y, size) |
size <- [1..300],
x <- [1..301-size],
y <- [1..301-size] ]
That works fine; it churns away a bit with high CPU but memory usage is modest.
Full code: https://github.com/mgritter/aoc2018/blob/master/day11/day11.hs